SAV
Conoscere Aedes.SAV
SOMMARIO
Aedes.SAV è un software per l'analisi e le verifiche di sicurezza di archi, volte e ponti in muratura fondato sui principi dell'analisi limite. Il software consente la valutazione statica dei sistemi voltati considerando anche eventuali interventi di rinforzo e con particolare attenzione alle verifiche di sicurezza sismica.
Le elaborazioni sono conformi alla Normativa tecnica vigente (D.M. 17.1.2018 e relativa Circolare 2019, Direttiva P.C.M. 9.2.2011 su valutazione e rischio sismico del patrimonio culturale, CNR-DT 213/2015: Istruzioni per la valutazione della sicurezza strutturale di ponti stradali in muratura, Linee guida 2022 per la Classificazione e Gestione del Rischio, la Valutazione della Sicurezza ed il Monitoraggio dei Ponti esistenti).

Le analisi implementate in SAV sono l'analisi limite e l'analisi elastica non lineare.
La metodologia di analisi limite è stata sviluppata dal Dipartimento di Costruzioni dell’Università degli Studi di Firenze, Facoltà di Architettura, autori: Prof. Arch. Michele Paradiso e Prof. Arch. Giacomo Tempesta, e si fonda sugli studi di Jacques Heyman, in accordo con le più avanzate ricerche del settore e supportata da indagini sperimentali. Nelle versioni successive, le attività di ricerca e sviluppo di Aedes Software, curate dall'Ing. Francesco Pugi, hanno esteso il campo di applicazione originario. Sono state sviluppate: l'analisi sismica con valutazione della vulnerabilità secondo le Normative di nuova generazione (DM 2018: indicatori di rischio sismico); l'analisi degli effetti dei cedimenti alle imposte orizzontali e/o verticali; l'analisi e la verifica di sicurezza dei ponti in muratura.
Con l'analisi limite vengono studiati gli SLU (Stati Limite Ultimi): EQU in Analisi Statica e SLV in Analisi Sismica.
Con l'analisi elastica non lineare, disponibile a partire dalla versione 2023, viene studiato SLE (Stato Limite di Esercizio); la metodologia consiste in un modello FEM ad aste e nodi, secondo le specifiche della CNR-DT 213/2015.
Per una descrizione completa delle procedure si rimanda alla manualistica di Aedes.SAV.
Si descrivono nel seguito alcuni aspetti significativi dell'analisi limite condotta secondo il modello implementato in SAV,
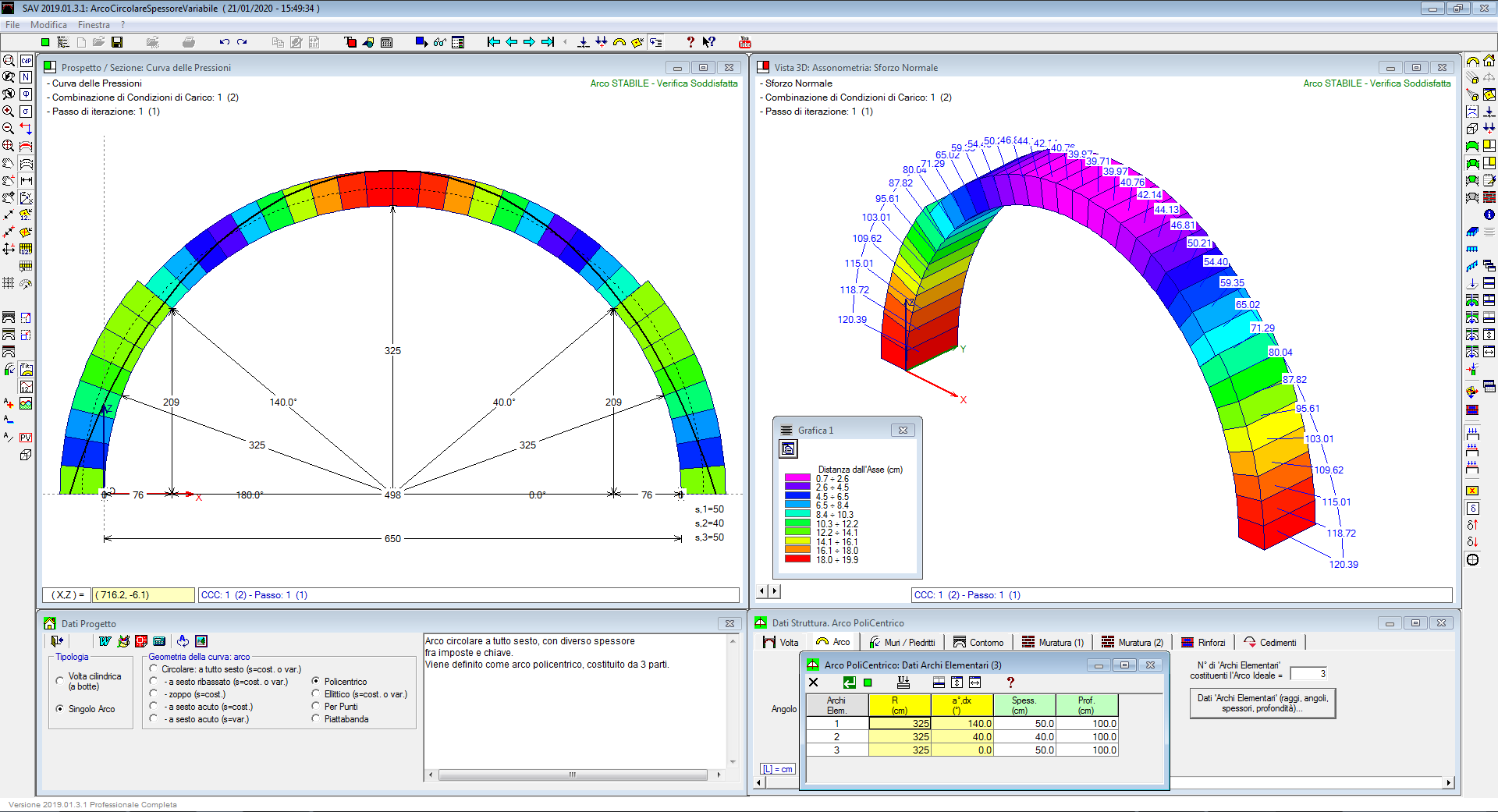
La struttura ad arco viene studiata considerandola composta da componenti rigidi, i conci, in grado di trasmettersi, attraverso le interfacce, soltanto sforzi di compressione. Viene in tal modo scritta una relazione complessiva di equilibrio, e tra le infinite soluzioni si ricerca l'esistenza di almeno una compatibile con le condizioni al contorno (curva delle pressioni interna alla sagoma dell'arco): se esiste, l'arco è stabile.
Se nel corso dell'analisi le condizioni di equilibrio determinano in una sezione la fuoriuscita della curva delle pressioni dalla geometria dell'arco, viene introdotta una cerniera che determina la tangenza della curva (in intradosso o in estradosso, a seconda dei casi).
Per passi iterativi è quindi possibile ricercare una condizione di equilibrio compatibile con l'assenza di trazioni nella muratura.
Qualora le cerniere siano introdotte in numero tale da determinare la formazione di un cinematismo (meccanismo di collasso) oppure più in generale non possano garantire una curva delle pressioni in equilibrio con i carichi, l'arco risulta instabile e quindi il controllo di sicurezza, sotto l'azione dei carichi applicati, non è soddisfatto.
Ne deriva un'indipendenza del calcolo dai moduli di elasticità della muratura: la verifica è di tipo geometrico, nell'ambito della statica grafica che da sempre ha guidato la concezione e la realizzazione di queste tipologie strutturali (ovviamente, i moduli di elasticità sono invece considerati nell'ambito dell'analisi elastica non lineare).
La sinergia fra la corretta impostazione di queste strutture (elementi rigido-fragili) e il moderno metodo agli elementi finiti liberano dalla necessità di presupporre schemi simmetrici o soggetti a carichi predeterminati o con posizioni di fessurazione (cerniere) definite a priori (come ad esempio nel metodo di Méry), consentendo pertanto un'analisi generalizzata che conduce anche ai moltiplicatori di collasso per carichi verticali e per azioni orizzontali. Quest'ultima opportunità è direttamente collegata all'analisi sismica della struttura.
Seguendo un'impostazione comune ai vari settori dell'analisi strutturale, i carichi (di superficie, lineari e concentrati, variamente disposti sull'estradosso della pavimentazione della volta) vengono definiti in Condizioni di Carico Elementari (CCE), e ad ogni carico è possibile associare l'effetto del moltiplicatore in direzione verticale o orizzontale.
Le CCE vengono combinate in Combinazioni di Condizioni di Carico (CCC); l'esecuzione dell'analisi risolve in una sola istanza tutte le CCC, ed esegue se richiesto il calcolo dei moltiplicatori di collasso.
I moltiplicatori di collasso riguardano sia i carichi verticali, per determinare il massimo valore compatibile con la sicurezza, sia gli orizzontali: questo è il caso della capacità sismica, ossia del moltiplicatore che segna la crisi della struttura (con instabilizzazione e possibile attivazione del meccanismo di collasso).
L'analisi sismica può essere eseguita considerando anche la componente sismica verticale. Le forze corrispondenti possono riferirsi al 100% oppure al 30% degli effetti, con forze disposte verso l'altro, verso il basso oppure dipendenti dal cinematismo. Le diverse ipotesi corrispondono a possibili combinazioni di contemporaneità fisica fra azioni orizzontali e verticali. La metodologia di calcolo considera che nel calcolo della capacità viene inserita, attraverso le forze verticali, la domanda e quindi un opportuno procedimento iterativo determina un risultato coerente relativamente al moltiplicatore sismico di collasso.
La valutazione della sicurezza in base alla stabilità rispetta le ipotesi tradizionalmente adottate per la verifica dei meccanismi per corpi rigidi:
- resistenza della muratura a trazione: nulla;
- scorrimento tra i blocchi (conci): assente;
- resistenza a compressione della muratura: infinita.
Per una valutazione più completa della sicurezza strutturale, conformemente alle indicazioni normative (§C8.7.1.2.1) in SAV è possibile considerare:
- gli scorrimenti tra i conci, svolgendo verifiche ad attrito (limitazione dell'azione tagliante in rapporto allo sforzo di compressione);
- la limitata resistenza a compressione della muratura, svolgendo le corrispondenti verifiche.
La mancanza di resistenza a trazione della muratura può essere compensata dai rinforzi: in SAV sono previste: catene, cappa in calcestruzzo in estradosso o in intradosso (fra cui lo spritz-beton; la cappa può avere armatura e quindi garantire resistenza a trazione), compositi in FRP e FRCM. Sia per la cappa, sia per i compositi è possibile impostare il tipo di calcolo come Verifica (eseguita sui dati in input) o Progetto (SAV progetta la dimensione del rinforzo strettamente necessaria, relativa al passo delle armature per la cappa in c.a. e all'estensione in profondità dell'arco del composito per FRP e FRCM), fermo restando che esigenze specifiche di cantiere, quali la realizzazione degli ancoraggi, possono talvolta determinare un prolungamento dei nastri fino anche ad interessare il completo sviluppo dell'arco.
E' inoltre disponibile in SAV la gestione delle spinte passive che consente un'analisi più appropriata nei casi in cui il meccanismo di collasso sia contrastato dalla reazione del riempimento nei confronti dello spostamento cinematico.
Per la verifica di ponti ad arco in muratura, SAV gestisce l'analisi di ponti esistenti in muratura, di tipo stradale o ferroviario, conformemente alla Normativa vigente: D.M. 17.1.2018 e Circolare 7 del 21.1.2019, linee guida CNR-DT 213/2015: "Istruzioni per la Valutazione della Sicurezza Strutturale di Ponti Stradali in Muratura", normative specifiche per i ponti ferroviari, Linee guida 2022 per i Ponti esistenti.
E' possibile definire automaticamente i carichi stradali e ferroviari secondo tali normative, attraverso appositi comandi che generano i corrispondenti carichi distribuiti e concentrati. Vengono gestite le spinte delle terre alle spalle. I ponti possono essere monocampata o pluricampata: nel caso dei pluricampata, opportuni comandi di interscambio delle azioni fra i file delle singole campate permettono di eseguire l'analisi con il metodo per 'componenti' nel rispetto delle Norme vigenti. Studi specifici sul rispetto delle regole dell'arte permettono di considerarne gli effetti sul fattore di confidenza. E' inoltre gestito il degrado strutturale, ai fini delle verifiche di resistenza.
Il software SAV consente inoltre la verifica dei piedritti, sottoposti sia in sommità alle azioni di imposta provenienti dagli archi, sia a forze aggiuntive; le forze aggiuntive possono provenire da archi di campate adiacenti. Queste modalità operative consentono, come sopra evidenziato, l'estensione del campo applicativo di SAV a volte consecutive e a ponti in muratura multicampata (i piedritti sono in tal caso spalle e/o pile).
Al moltiplicatore orizzontale delle masse viene associata, secondo la metodologia indicata dalla Normativa vigente (Circ. 7 del 21.1.2019: §C8.7.1.2.1) la capacità in termini di periodo di ritorno TR o di accelerazione al suolo PGA, con definizione dell'Indicatore di Rischio Sismico ζE, consistente nel rapporto tra Capacità e Domanda.
Viene infine definita la capacità della struttura in termini di Vita Nominale VNC, valutazione richiesta dalla Direttiva P.C.M 9.2.2011 sui beni monumentali, §2.4.
L'analisi strutturale con il software SAV è completata dallo studio degli effetti prodotti dal movimento delle imposte:
- in analisi statica, ad esempio spostamenti verticali dovuti a cedimenti di fondazione;
- in analisi sismica:
- traslazione verticale: abbassamento o innalzamento per effetti sismici verticali,
- traslazione orizzontale: allontanamento reciproco delle imposte per deformazioni asincrone delle pareti murarie su cui la struttura ad arco si imposta; negli eventi sismici è questa una delle cause più frequenti di crisi delle volte sottili.
La documentazione di SAV include una serie di esempi applicativi, e per la validazione viene fatto riferimento a specifiche pubblicazioni sull'argomento; in particolare il volume:
"Sistemi Voltati in Muratura: Teoria e applicazioni", autori: Paradiso M., Tempesta G., Galassi S., Pugi F., 2007, DEI, Tipografia del Genio Civile, i cui contenuti applicativi sono confluiti nella documentazione del software SAV.

Un estratto dalla Presentazione del libro, a cura di Michele Paradiso e Giacomo Tempesta:
"La prevenzione del rischio sismico, la salvaguardia dei centri storici, il consolidamento dei monumenti, sono temi attuali di dibattito che investono la quotidianità della professione dell'architetto e dell'ingegnere.
Nel presentare uno strumento di calcolo per le strutture voltate in muratura (SAV), gli autori si preoccupano non solo di evidenziarne le caratteristiche e le potenzialità, ma soprattutto di fornire al lettore-utente una panoramica, sintetica e non certo esaustiva, dello sviluppo storico del pensiero scientifico sul comportamento di archi e volte in muratura, a partire dal XVII secolo. (...) Nella prima parte, partendo da Coulomb, Méry, Castigliano si arriva all'opera fondamentale di Jacques Heyman, dalla quale traggono origine gli studi e le ricerche che hanno portato alla concezione dell'algoritmo.
La seconda parte si dedica a mostrare e a discutere esempi di applicazioni pratiche del software, includendo utili riferimenti alle normative vigenti".
Teoria statica generale
Paradiso M., Tempesta G., Galassi S., Pugi F.: “Sistemi Voltati in Muratura”, DEI Tipografia del Genio Civile, Roma, 2007
Paradiso M., Tempesta G.: “Archi, Volte e Cupole: Analisi e Calcolo”, in "Archi e volte in zona sismica, Meccanica delle strutture voltate", a cura di Antonio Borri e Laura Bussi, Edizioni Doppiavoce, Napoli, 2011, ISBN 978-88-89972-28-1, pagg. 81-157
Paradiso M., Tempesta G., Galassi S.: “X-Vaults: a Software for the Analysis of the Stability of Masonry Cross-Vaults”, International Journal of Computer Science Issues, Vol.9, Issue 2, No.2, March 2012, ISSN (Online): 1694-0814
Briccoli Bati S., Paradiso M., Tempesta G.: "Sul calcolo degli archi in muratura", Dipartimento di Costruzioni, Facoltà di Architettura, Università degli Studi di Firenze
Briccoli Bati S., Paradiso M., Tempesta G.: "Analisi statica e cinematica ed equilibrio limite di strutture ad arco a vincoli unilateri", Atti del IX Convegno Nazionale dell'Associazione Italiana di Meccanica Teorica e Applicata (AIMETA)
Applicazioni della Normativa tecnica
Pugi F., Galassi S.: "Seismic analysis of masonry voussoir arches according to the Italian building code", Int. J. Earthquake Eng. 2013;30(3):33-55
Cedimenti
Galassi S., Misseri G., Rovero L., Tempesta G.: "Failure modes prediction of masonry voussoir arches in moving supports", Engineering Structures 173 (2018), 706-717
Spinte passive dal riempimento sopra la volta
Gelfi P.: "Role of Horizontal Backfill Passive Pressure on the Stability of Masonry Vaults", Restoration of Buildings and Monuments 8 (2002): 573 - 590
Ponti esistenti in muratura
Mazzoleni M., Jurina L.: "Ponti in muratura: difetti e patologie", Convegno CIAS: Ponti e viadotti: ispezioni visive e tecniche di risanamento, Bolzano, 18-19 ottobre 2006
Da Porto F.: "Vulnerabilità sismica dei ponti ferroviari in muratura", Convegno CIFI, RFI - Università degli Studi di Padova, 2013
M. Corradi: "Empirical methods for the construction of masonry arch bridges in the 19th century". Arch Bridges: history, analysis, assessment, maintenance and repair. Proceedings of the second international arch bridge conference, Edr A. Sinopoli, Venice 6-9 October 1998, Balkema Rotterdam, pp 25-36
D. Proske, Pieter van Gelder: "Safety of Historical Stone Arch Bridges", Springer, 2009
Per conoscere in modo completo SAV, puoi consultare i manuali:
Manuale di SAV
Vol. 1: Teoria
Vol. 2: Manuale d'uso
Vol. 3: Esempi applicativi
1. Geometria dell'arco e della volta
2. Muri e piedritti
3. Strutture al contorno
4. Rinforzi
5. Carichi
1. GEOMETRIA DELL'ARCO E DELLA VOLTA
Geometria degli archi: circolare a tutto sesto, con spessore costante o variabile; a sesto ribassato (con spessore costante o variabile); zoppo; a sesto acuto (con spessore costante o variabile); policentrico; ellittico (con spessore costante o variabile); definito per punti (curvatura generica in input per punto o via file dxf); piattabanda.
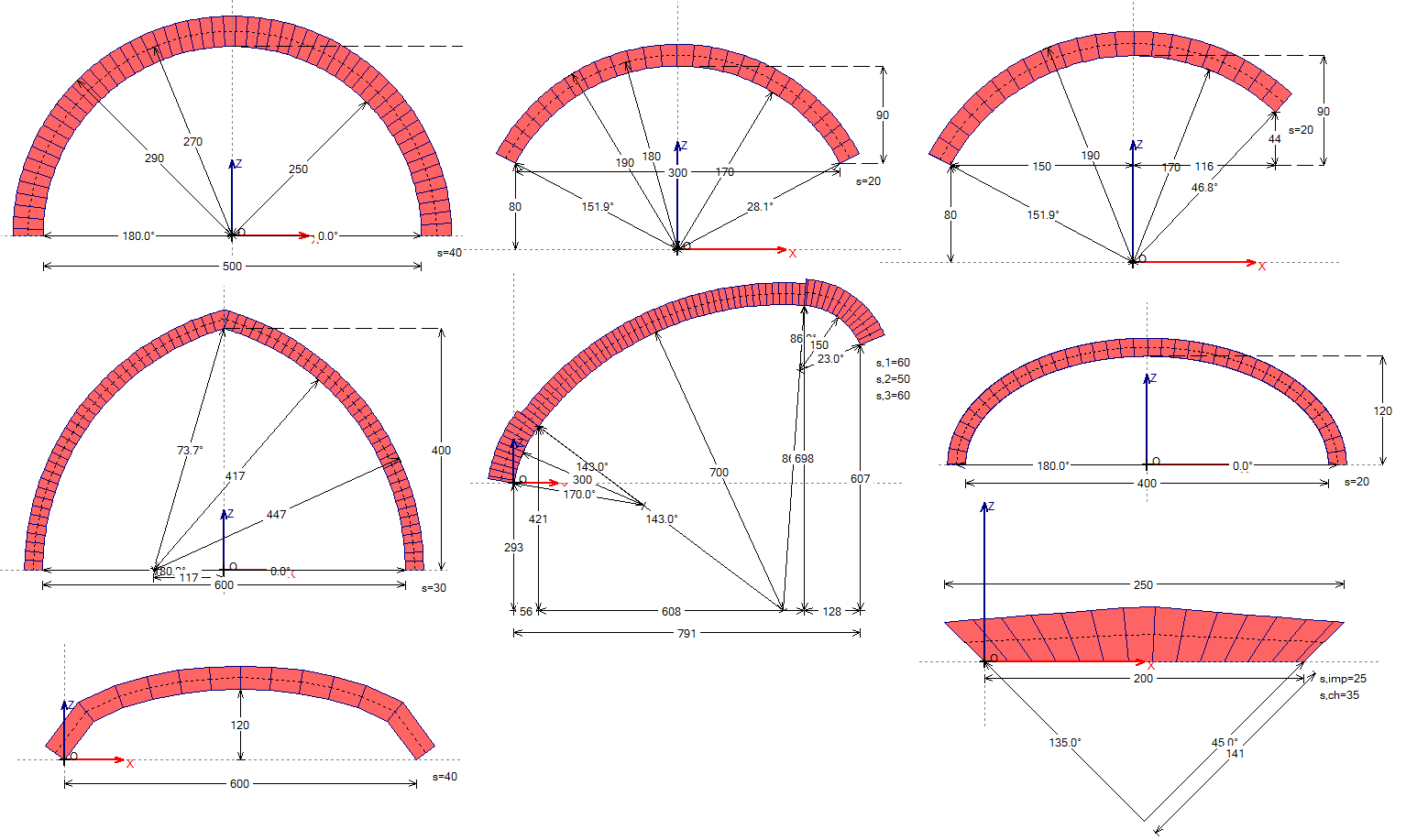
L'arco definito per punti può avere spessore e profondità variabili: ciò consente la modellazione di archi derivanti dalla scomposizione di volte spaziali a doppia curvatura.
Ad esempio, per una volta a crociera verranno studiati gli archi diagonali e i perimetrali; anche per una volta a vela la scomposizione riconduce ad archi diagonali e perimetrali.
L'insieme degli archi derivanti dalla scomposizione garantisce di fatto un'analisi a favore di sicurezza.
Si consideri ad esempio la volta a vela dell'immagine seguente.
La volta a vela è costituita da una struttura di tipo semisferico sezionata da piani verticali, passanti per i muri o i pilastri di imposta. La volta risulta delimitata da archi perimetrali impostati sui pilastri o sui muri (a); sezionandola con un piano orizzontale passante per la chiave degli archi, la volta viene suddivisa in una calotta e in quattro pennacchi sferici (b). La volta a vela è una volta a doppia curvatura che copre generalmente un vano a pianta quadrata, ma la pianta può anche essere rettangolare.
Con SAV è possibile modellare gli archi diagonali (1) e (2) e gli archi longitudinali e trasversali (3) e (4).
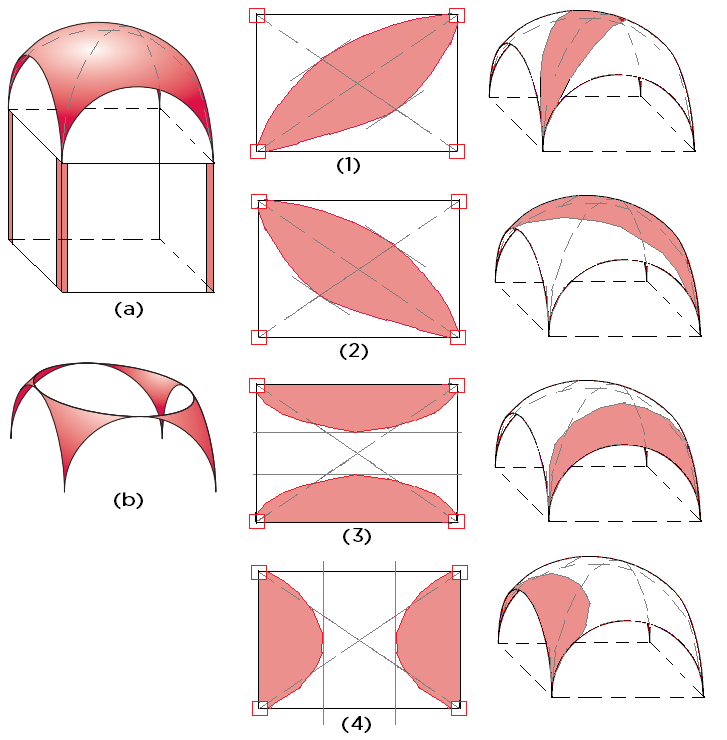
L'arco diagonale, ad esempio, è un arco piano (a tutto sesto in caso di calotta perfettamente semisferica) avente profondità variabile crescente dall'imposta verso la chiave, ed una forma simmetrica rispetto all'asse verticale centrale.
Per quanto riguarda i carichi agenti su archi definiti per punti, quali quelli a profondità variabile, oltre ai pesi propri SAV consente l'input di una sequenza di carichi concentrati variabili dall'imposta verso la chiave, adeguatamente valutati dal Progettista.
Nell'immagine seguente si riporta un esempio di modellazione di arco a tutto sesto con spessore costante (lo spessore della muratura resistente della volta) e con profondità e carichi variabili, agevolata da operazioni preliminari su CAD per la determinazione delle
coordinate dei conci (da inserire nei dati dell'Arco per punti di SAV) e delle loro profondità:
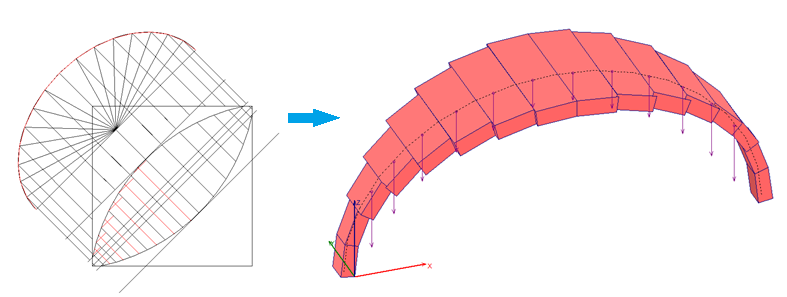
Negli schemi strutturali si può tenere conto dello spessore murario massiccio che la volta a vela presenta in corrispondenza dell'imposta evitando nell'arco diagonale a tutto sesto la schematizzazione del primo concio, in posizione quasi verticale: nel modello teorico tale concio può infatti richiedere l'inserimento di una cerniera, come accade tipicamente negli schemi a tutto sesto, aventi minore grado di stabilità rispetto ai ribassati, e questa cerniera può condurre ad un'instabilità più teorica che reale. Con SAV è possibile modificare lo schema strutturale dell'arco, ad esempio rimuovendo il primo concio, ricercando così, se è possibile, una soluzione stabile.
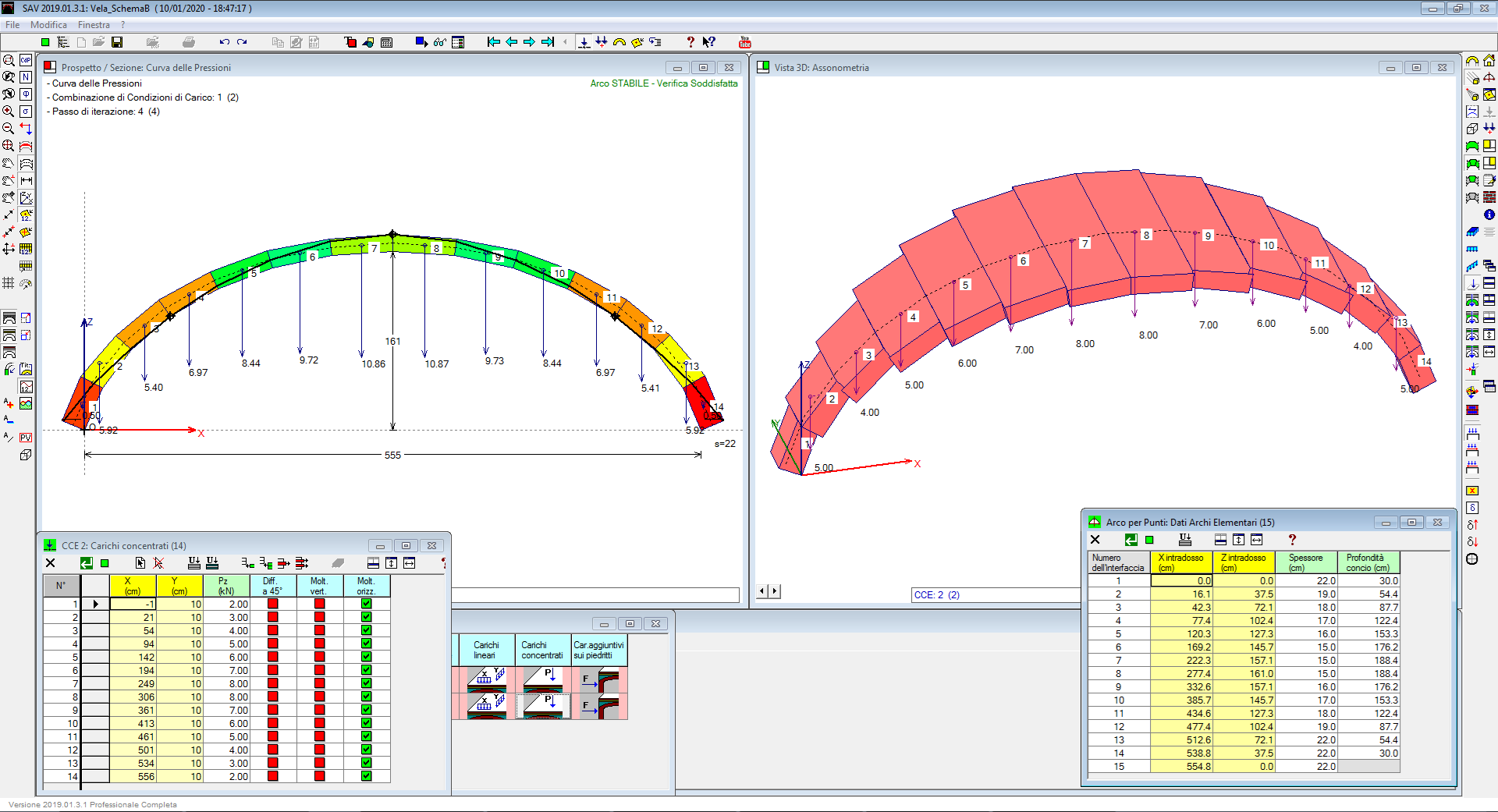
Per una cupola (in figura seguente) la modellazione viene eseguita estraendo un arco a sezione trasversale con profondità variabile, in diminuzione dall'imposta verso la sommità tale da rappresentare lo spicchio elementare.
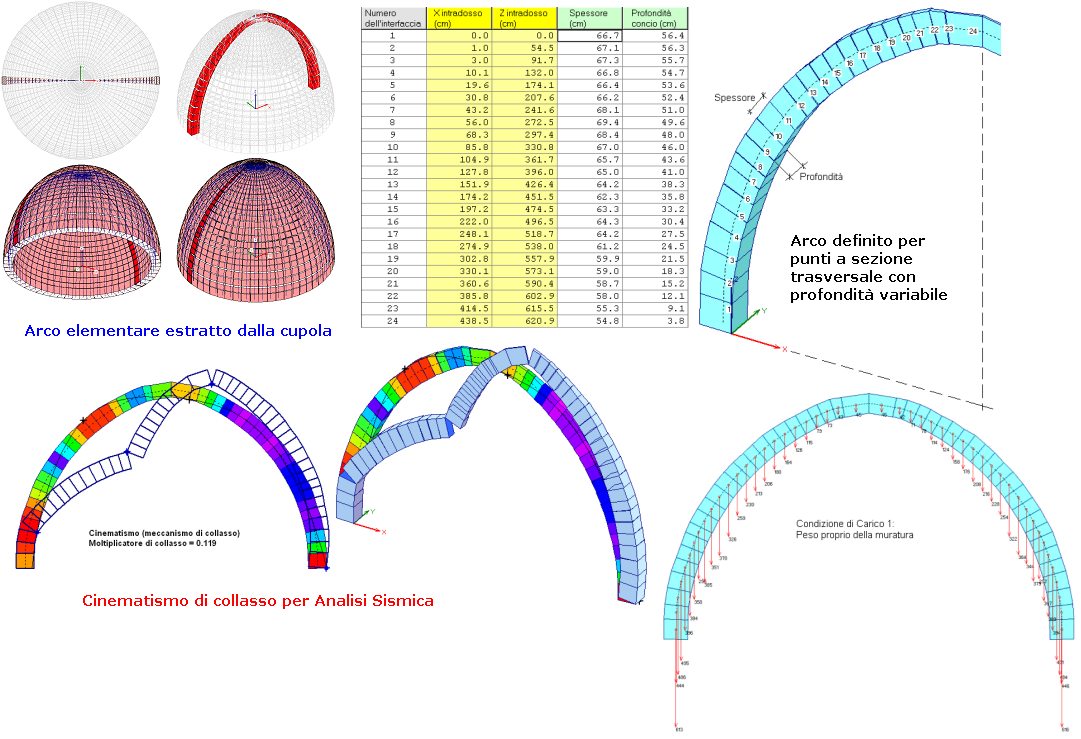
Oltre alla geometria dell'arco o della volta, in SAV vengono definite le strutture al contorno (rinfianchi o riempimento, sottofondo, pavimentazione) e i piedritti o muri, su cui l'arco si imposta. Altri dati riguardano i parametri meccanici dei materiali e gli eventuali rinforzi.
In input sono disponibili anche dati riguardanti eventuali cedimenti delle imposte.
Attraverso i Parametri di Calcolo vengono specificati i dati sull'azione sismica e su altre impostazioni di modellazione e analisi. Infine, i carichi descrivono le azioni applicate sulla struttura.
2. MURI E PIEDRITTI
Strutture d’imposta della volta: muri (nel caso di struttura voltata estesa) o piedritti (corrispondenti al caso del singolo arco). In input: altezza; tipologia della sezione (rettangolare, circolare, ottagonale); posizione rispetto all’imposta dell’arco; dimensioni della fondazione. Nell'immagine seguente: verifica del sistema arco - piedritti.
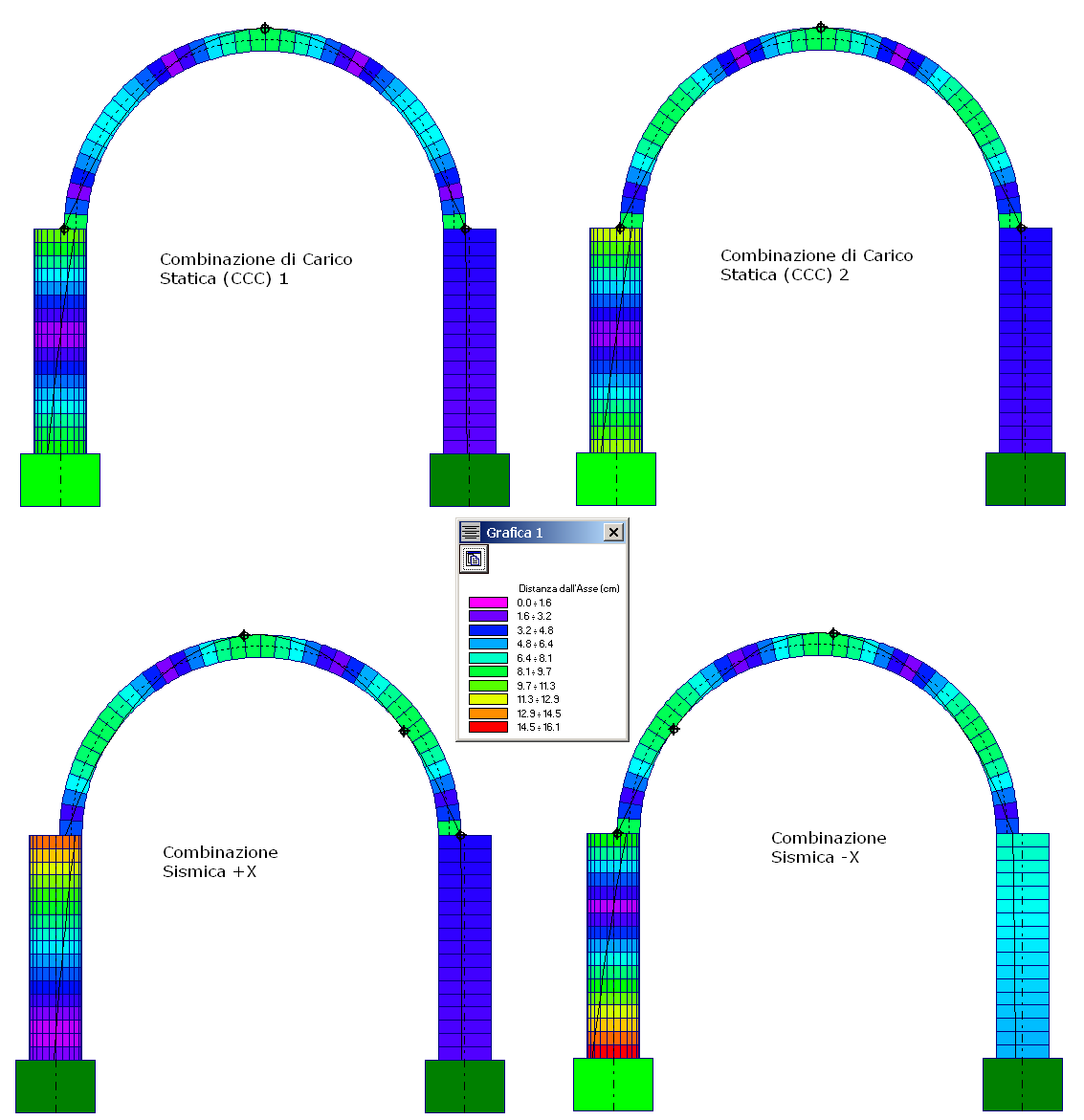
3. STRUTTURE AL CONTORNO
Rinfianchi (o riempimento), sottofondo, pavimentazione.
I rinfianchi (o riempimento) sono definiti dal volume sovrastante l’arco fino al massimo alla quota di estradosso in chiave (o fino ad una quota inferiore rispetto alla linea orizzontale di chiave.
Si parla, più propriamente, di ‘rinfianchi’ quando la struttura di contorno assume valenza strutturale, mentre il ‘riempimento’ corrisponde a materiale avente semplicemente la funzione di peso sull’arco. E’ noto che il peso del rinfianco o riempimento svolge un ruolo generalmente benefico sulla statica dell’arco, stabilizzandone la curva delle pressioni (anche se una massa eccessiva può non essere favorevole per il comportamento sismico della struttura). Le strutture sovrastanti (sottofondo, pavimentazione) si impostano sopra la linea di chiave dell’arco.
Lo spessore di sottofondo e/o pavimentazione può contribuire alla diffusione dei carichi applicati, pensati agenti sulla superficie superiore della struttura (quindi, p.es. sopra la pavimentazione). Un carico generico (di superficie, lineare o concentrato) verrà infatti diffuso a 45° entro tale spessore, qualora la corrispondente opzione sia attivata nella definizione del carico stesso (nell’ambito di definizione delle CCE).
Oltre a fornire 'peso', ossia carico verticale, si può considerare che il riempimento svolga un ruolo più importante contrastando la deformazione generata dall'attivazione del cinematismo.
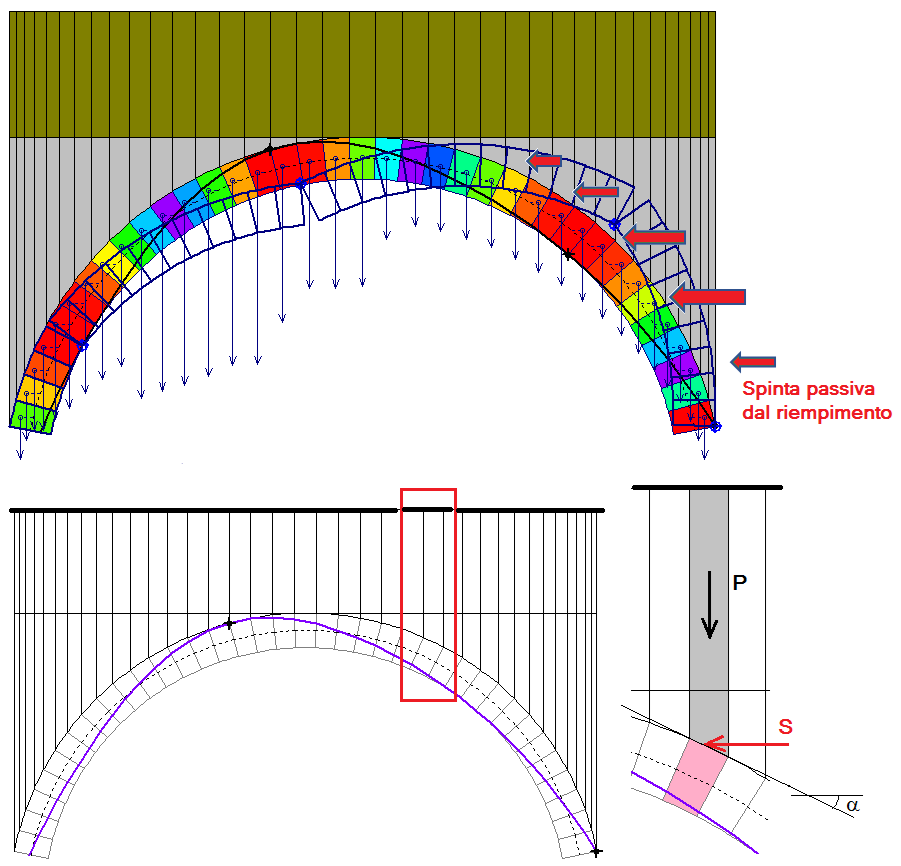
Alcuni Autori (Mazzoleni e Jurina, vd. Riferimenti bibliografici) hanno condotto indagini parametriche grazie alle quali è stato posto in rilievo "il fondamentale ruolo svolto dai rinfianchi, e più in generale dalla sovrastante massa muraria, nei confronti del comportamento ultimo dell'arco portante. L'apporto fornito da tali elementi non è limitato alla sola spinta verticale del peso proprio, ma si esplica anche in termini di spinta orizzontale, con una importante funzione di 'contenimento' nei confronti di un eventuale cinematismo dell'arco." Questo effetto stabilizzante "è subordinato all'esistenza di alcune fondamentali condizioni al contorno fra cui: la presenza di rinfianchi compatti e dotati di buone caratteristiche meccaniche; la presenza di imposte in grado di sopportare l'incremento di spinta orizzontale derivato dalla spinta passiva del rinfianco".
In SAV la gestione delle azioni dovuti alle spinte passive consente un'analisi più appropriata nei casi in cui il meccanismo di collasso sia contrastato dalla reazione del riempimento nei confronti dello spostamento cinematico.
Un apposito comando della finestra dei Carichi Concentrati della CCE corrente calcola ed applica automaticamente le azioni orizzontali da spinta passiva sui conci, distinguendo la metà a monte (a sinistra dell'asse verticale dell'arco) da quella a valle (a destra dell'asse verticale) e rendendo inoltre possibile la selezione dell'azione passiva solo su un gruppo di determinati conci.
4. RINFORZI
Le strutture di rinforzo sono distinte in due gruppi:
- rinforzi di superficie, che interessano la superficie di intradosso o di estradosso dell’arco;
- rinforzi puntuali, caratterizzati da catene o rinforzi localizzati.
Le catene negli archi possono essere inserite contemporaneamente agli altri rinforzi di superficie o localizzati.
Nella scheda Rinforzi è possibile specificare alternativamente tre tipologie:
- cappa in calcestruzzo;
- nastri in FRP, posti in estradosso oppure in intradosso;
- rinforzi a trazione localizzati su una o più interfacce tra i conci, in estradosso o in intradosso. L’elaborazione di calcolo prevede in tal caso la possibilità di definire le superfici di nastro ottimali, necessarie a garantire la verifica di resistenza a trazione (un esempio è riportato in figura seguente).
5. CARICHI
I dati sui Carichi vengono suddivisi in: Condizioni di Carico Elementari (CCE), e Combinazioni di Condizioni di Carico elementari (CCC).
CCE (Condizioni di Carico Elementari)
I carichi sono articolati in: carichi di superficie, lineari e concentrati. I carichi di superficie e distribuiti lineari insistono sull'estradosso delle strutture sovrastanti l'arco (rinfianchi con eventualmente sottofondo e pavimentazione); i carichi concentrati possono anch'essi essere applicati sull'estradosso delle strutture sovrastanti l'arco o in alternativa direttamente su specifici conci. I carichi di superficie sono verticali; i carichi lineari e concentrati sono caratterizzati dalle due componenti verticale e orizzontale.
Per ognuno dei carichi applicati superiormente alle strutture è possibile specificare se eseguire la diffusione a 45° nello spessore sovrastante la linea di chiave (spessore determinato da sottofondo e/o pavimentazione). Per ognuno dei carichi è possibile inoltre specificare se è affetto da moltiplicatore verticale e le analisi nelle quali deve essere considerato (statica, sismica +X, sismica -X).
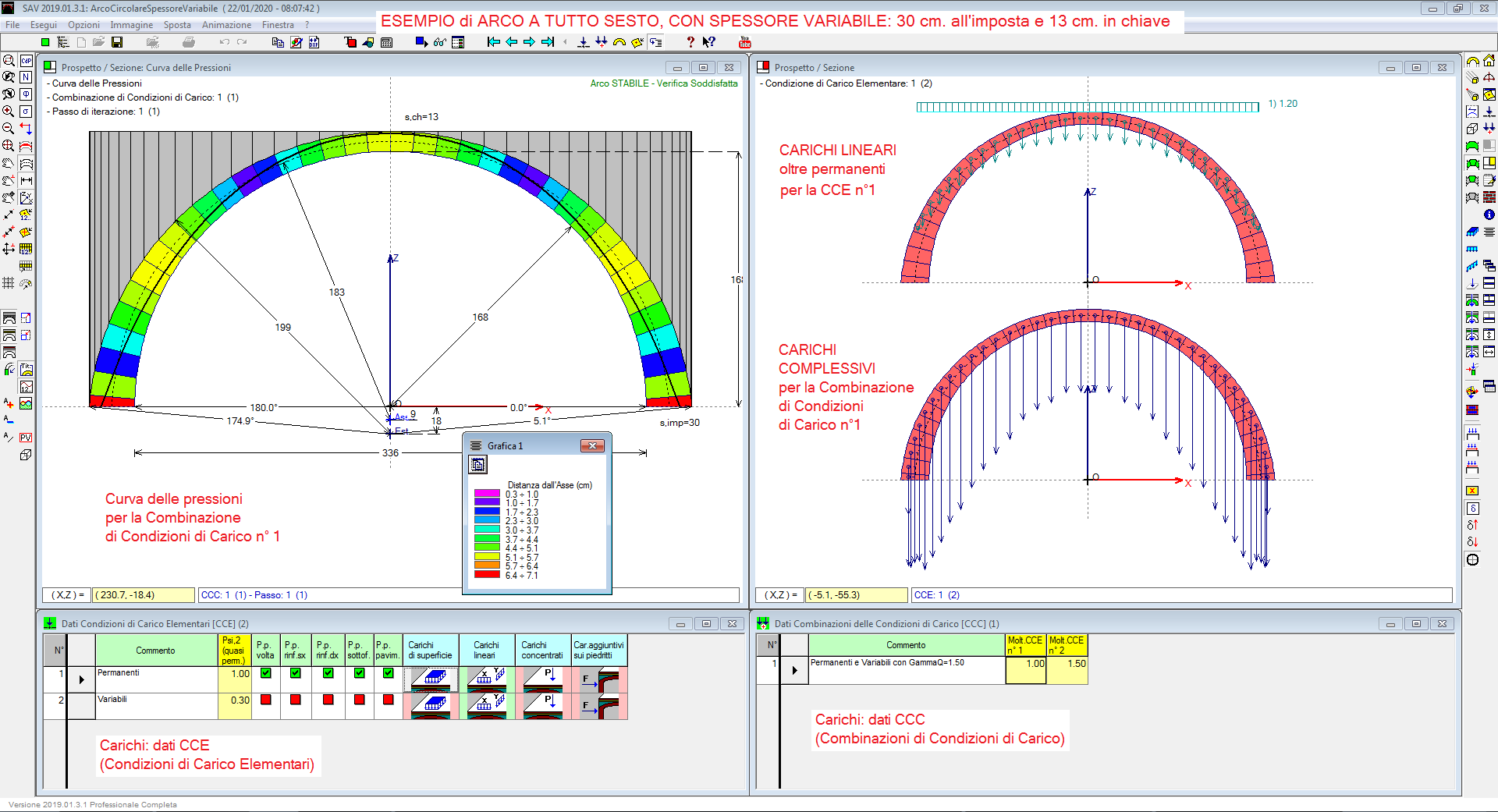
CCC (Combinazioni delle Condizioni di Carico elementari)
L'Analisi Statica viene eseguita per tutte le CCC (Combinazioni delle Condizioni di Carico elementari) specificate. E’ possibile studiare anche più tipi di combinazioni (p.es. con rinfianchi solo da un lato, o con alcuni carichi piuttosto che altri).
Per ogni CCC si può calcolare, se richiesto nei Parametri di Calcolo, il moltiplicatore di carico verticale.
L'Analisi Sismica viene eseguita per la sola Combinazione Sismica, definita secondo la Normativa vigente ([2.5.5] in §2.5.3, D.M. 17.1.2018). Ai carichi verticali sismicamente attivi (corrispondenti a masse) corrispondono forze inerziali orizzontali, che vengono composte con le eventuali forze orizzontali (ad esempio, le spinte passive dal riempimento). Ad ogni condizione di carico elementare vengono applicati i corrispondenti coefficienti di combinazione ψ2.
La struttura, vista come volta, può essere suddivisa in più archi, ed i carichi di superficie, lineari o concentrati su di essa applicati verranno ripartiti sugli archi intercettati in base alla posizione geometrica dei carichi stessi.
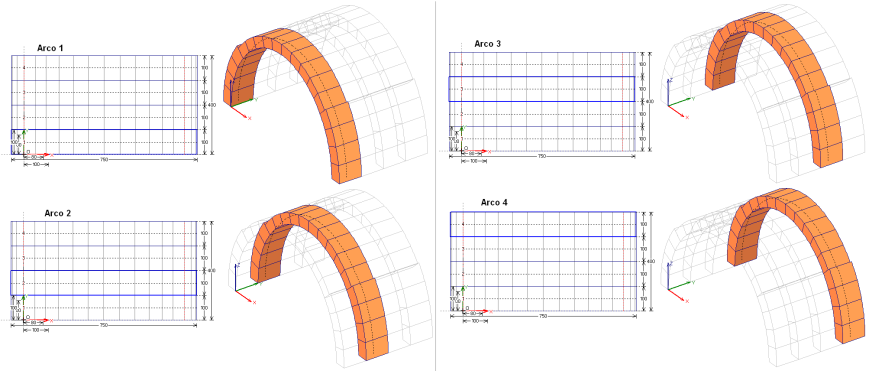
Un esempio di carico di superficie e delle azioni sui conci da esso trasmesse su uno degli archi costituenti la volta è rappresentato nell'immagine seguente.
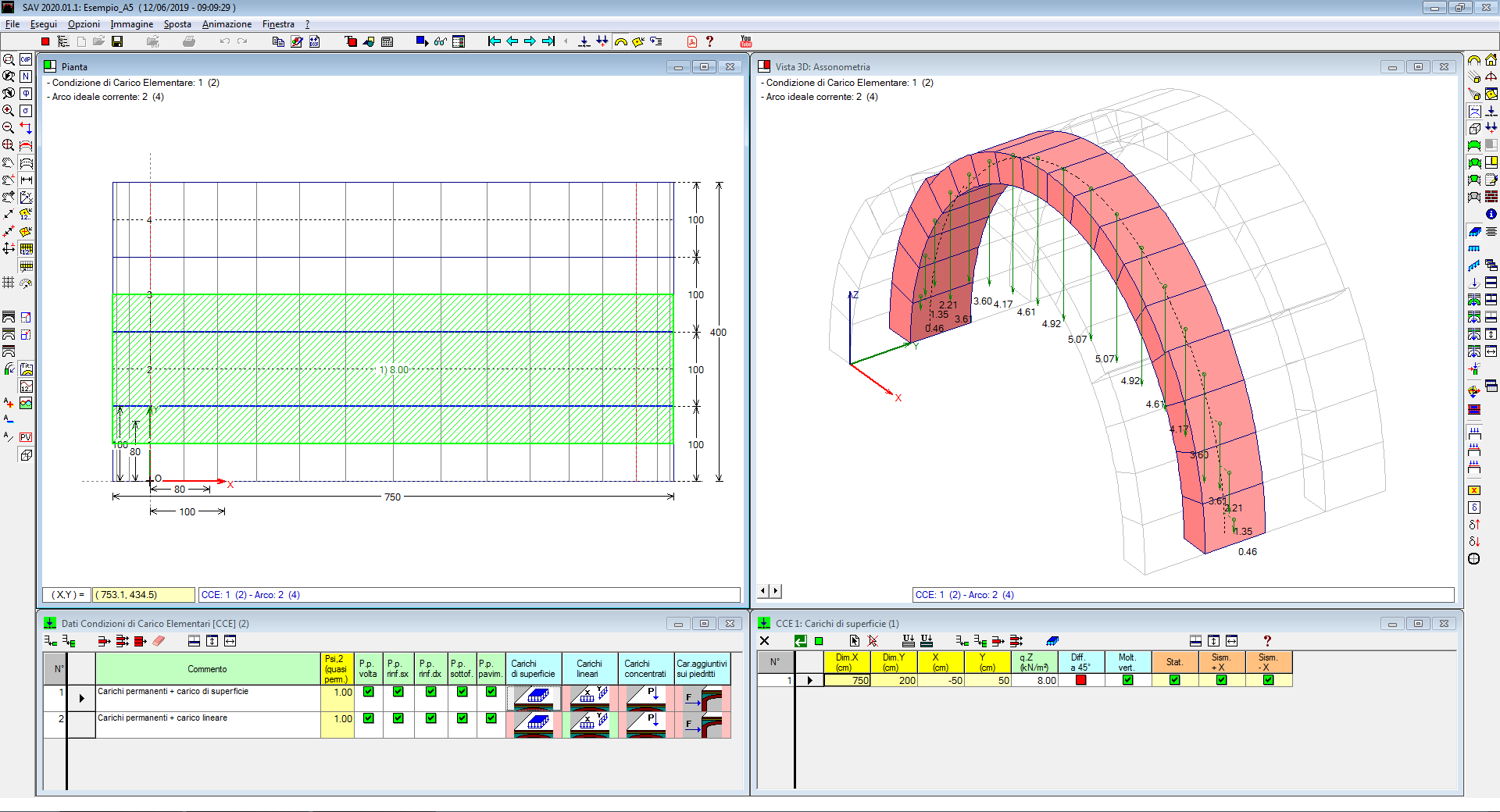
Nell'analisi di strutture voltate composte da più archi, il moltiplicatore di collasso, sia per carichi verticali, sia per carichi orizzontali, viene determinato come minimo valore fra tutti i moltiplicatori calcolati per i singoli archi costituenti la volta, distintamente fra le tre analisi Statica, Sismica +X, Sismica -X.
L'Analisi Statica viene eseguita per tutte le CCC (Combinazioni delle Condizioni di Carico elementari) specificate. Le CCC vengono composte a partire dalla CCE applicando corrispondenti moltiplicatori.
Se richiesto nei Parametri di Calcolo, per ogni CCC contenente carichi affetti da moltiplicatore verticale, si calcolerà il moltiplicatore di collasso verticale.
In SAV vengono eseguite quattro verifiche fondamentali:
- equilibrio della struttura (verifica di stabilità) (sempre eseguita),
- verifica ad attrito (taglio nei giunti, in corrispondenza delle interfacce) (opzionale),
- verifica a compressione della muratura (opzionale),
- verifica a trazione dei rinforzi (nel caso di struttura consolidata).
La verifica di stabilità viene eseguita applicando la metodologia di analisi limite già illustrata, finalizzata alla ricerca di una configurazione equilibrata con i carichi nel rispetto delle condizioni al contorno (curva delle pressioni interna alla sagoma dell'arco), in grado di garantire l'assenza di trazioni nella muratura.
La stabilità dell’equilibrio può essere assicurata dalla formazione di una o più cerniere, con perdita di altrettanti gradi di iperstaticità.
Se l'arco è stabile, risulta definito un campo di sollecitazioni nei conci e nelle imposte; sono quindi noti gli sforzi nelle bielle di intradosso e di estradosso (cui corrisponde lo sforzo normale N) e di taglio nella biella d'interfaccia, nonché le azioni alle imposte (carico verticale e spinta).
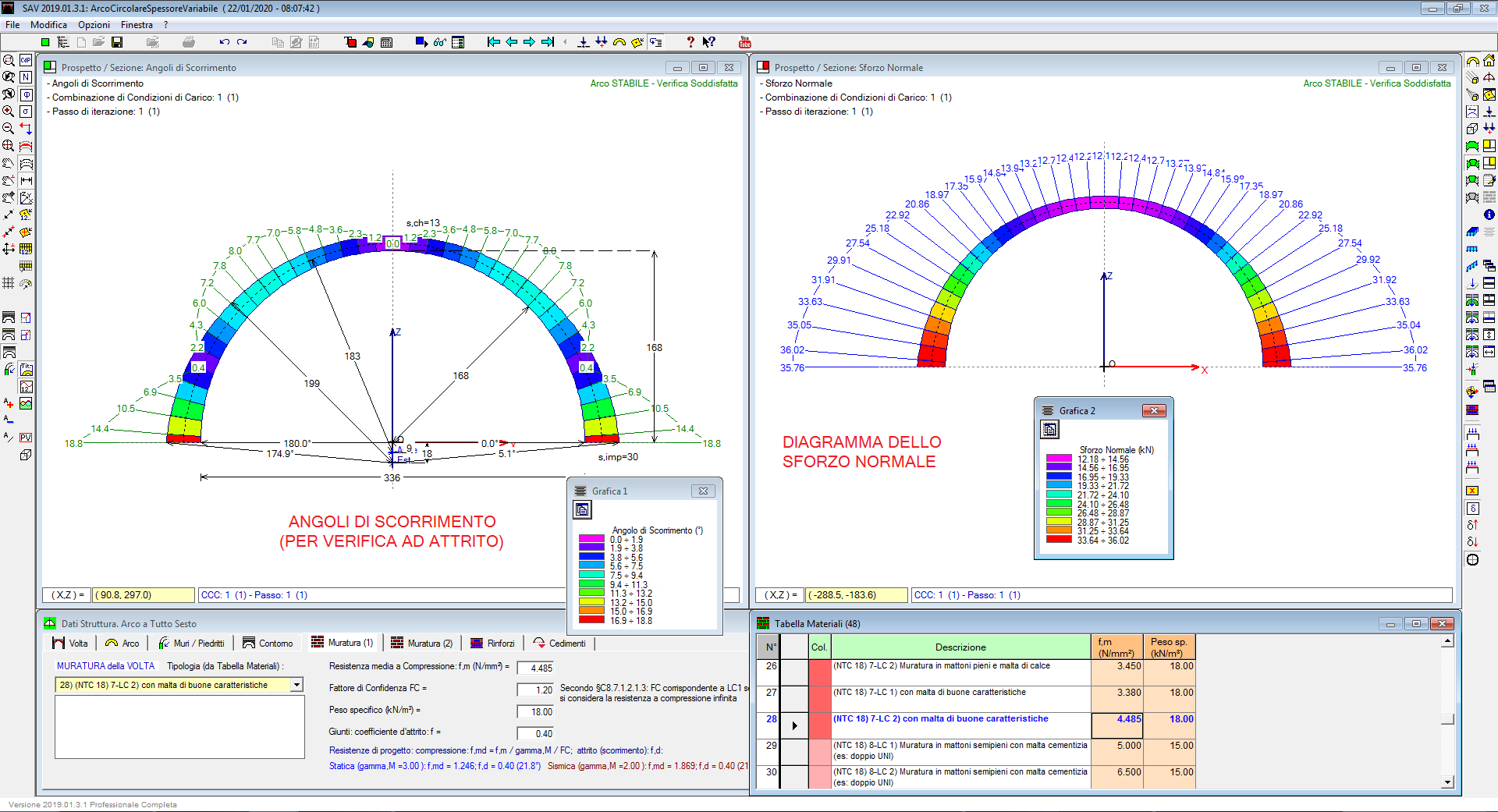
La verifica ad attrito è soddisfatta quando in ogni interfaccia il taglio T risulta inferiore alla resistenza per attrito ( f N ), dove N è lo sforzo normale agente sulla sezione e f è il coefficiente di attrito della malta interposta fra i mattoni o i conci di pietra, o del concio sul concio nel caso di assenza di interposizione di malta (conci in mutuo contrasto tra loro).
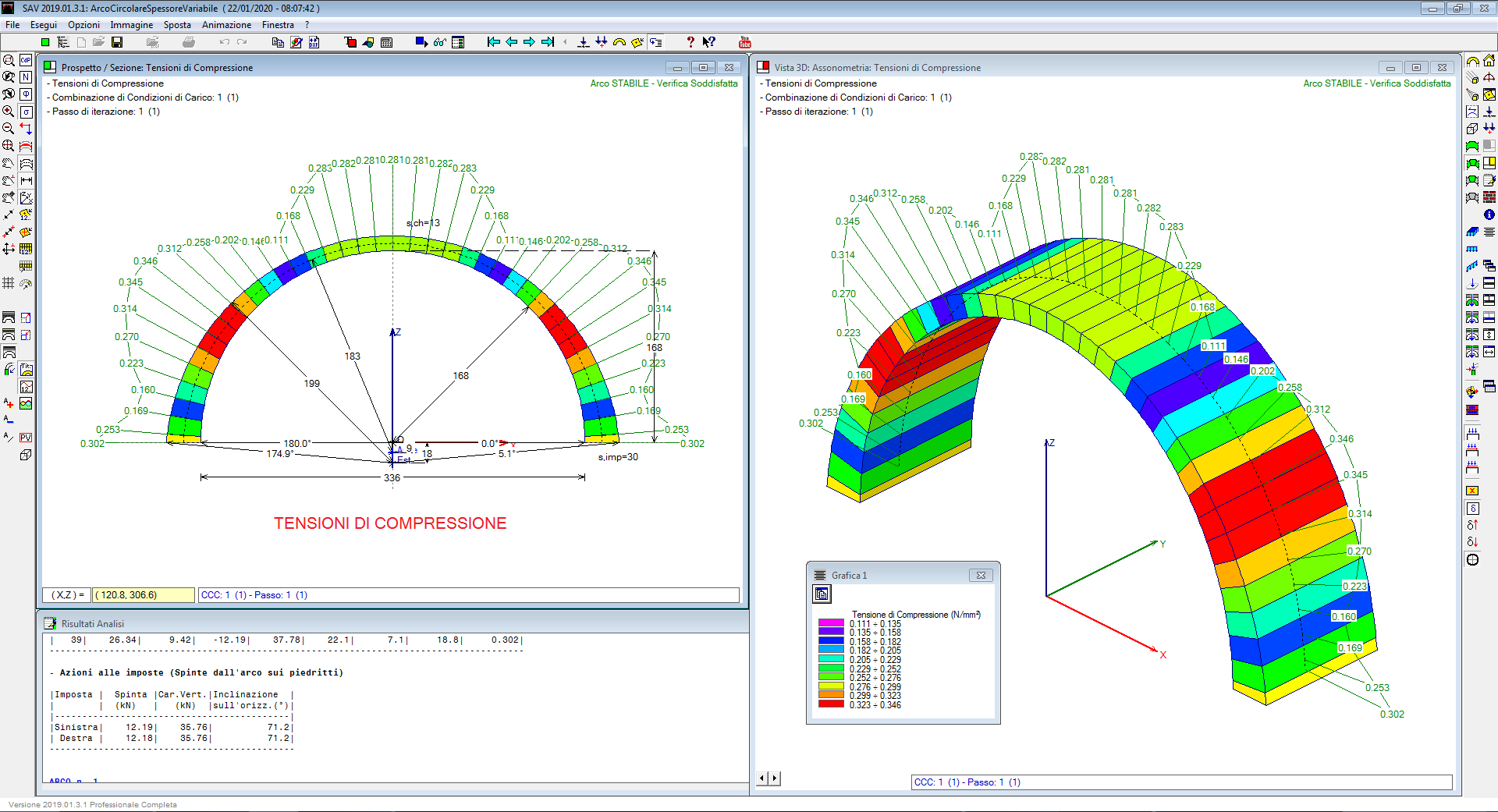
Per la verifica a compressione, la tensione viene calcolata nell’ipotesi di diagramma trapezoidale se lo sforzo normale è interno al nocciolo d’inerzia, triangolare con sola resistenza a compressione (quindi con zona reagente minore della dimensione della sezione) se lo sforzo normale è esterno al nocciolo d’inerzia. In corrispondenza delle sezioni dove è presente trazione, sia nel caso di rinforzo che non, la massima tensione nella muratura viene calcolata adottando lo schema uniforme (rettangolare), distribuendovi lo sforzo normale agente nella biella compressa. Ciò equivale quindi a supporre che lo schiacciamento della muratura nella realtà non sia 'puntuale' ma interessi uno spessore dell'arco, supposto pari a s/3, secondo indicazioni provenienti dalla Ricerca sperimentale.
La verifica a trazione dei rinforzi viene eseguita solo se è stata definita una struttura associata alla muratura in grado di reagire a trazione, sia essa una catena piuttosto che una cappa in calcestruzzo armato o nastri in composito fibrorinforzato o ancora: rinforzi a trazione localizzati.
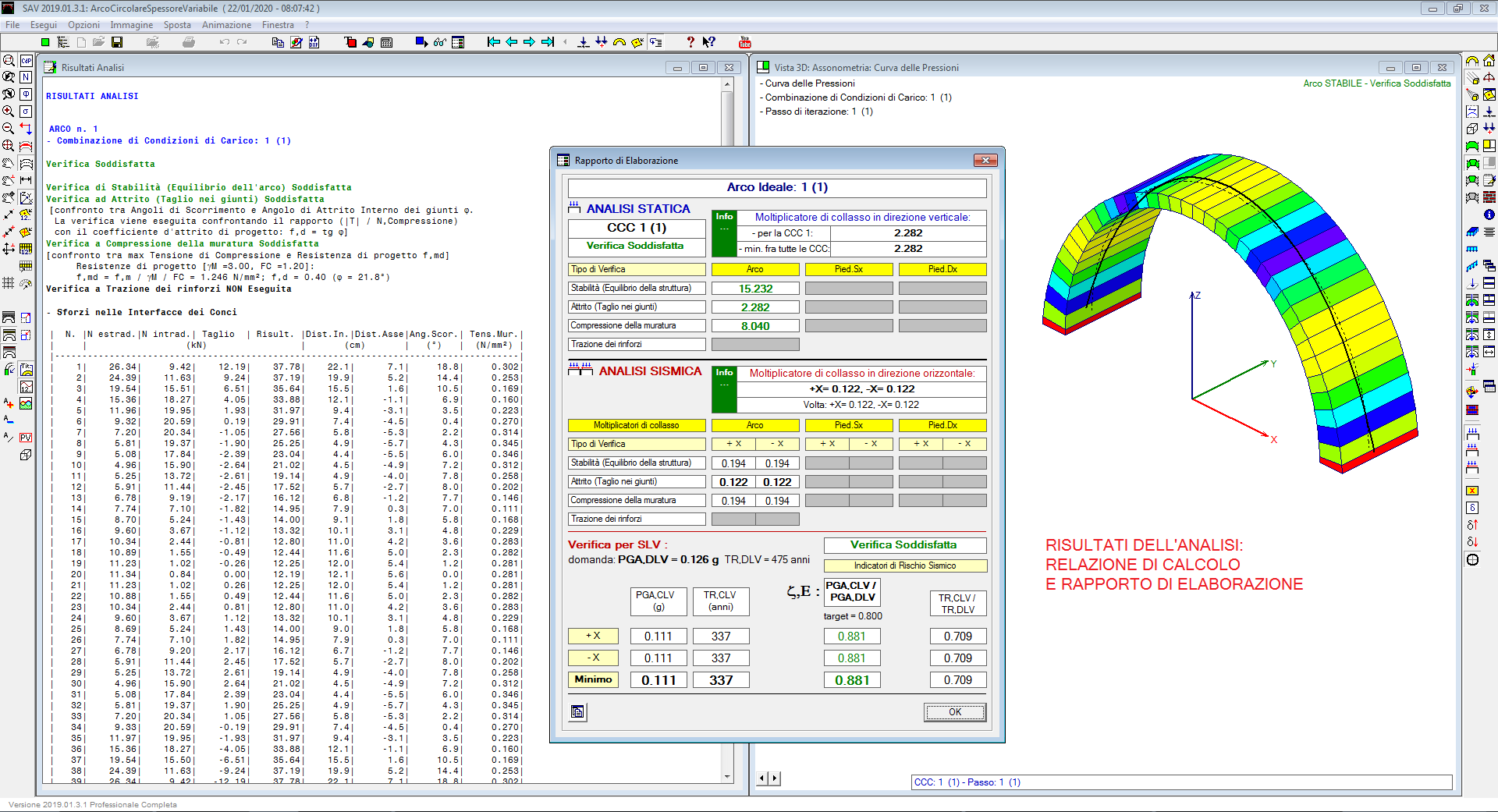
Eseguendo l'elaborazione di calcolo, vengono risolti in una sola istanza tutti i singoli archi della volta per tutte le CCC e per entrambe le analisi statica e sismica, con determinazione dei moltiplicatori di collasso.
I risultati sono riassunti nel rapporto di elaborazione e mostrati in dettaglio nella relazione di calcolo.
Nel rapporto di elaborazione vengono evidenziati, qualora richiesti, anche i valori del moltiplicatore di collasso verticale.
Ai carichi competenti a pesi propri non viene ovviamente attribuito un moltiplicatore verticale: esso si riferisce a carichi aggiuntivi di natura variabile (talvolta anche a permanenti dei quali si desideri valutare la massima intensità sostenibile).
Il moltiplicatore di collasso per carichi verticali dipende in primo luogo dalla stabilità, ossia dall'influenza dell'intensità dei carichi sull'equilibrio dell'arco.
Frequentemente i valori del moltiplicatore di collasso possono essere elevati: ciò conferma quanto noto, ossia che l'aumento del carico e quindi della compressione nella struttura ad arco - almeno entro certi limiti - non è sfavorevole nei confronti della stabilità. Dal punto di vista ingegneristico, può comunque risultare opportuna una limitazione superiore ai valori del moltiplicatore di collasso offerta dalle verifiche di resistenza per attrito e/o compressione.
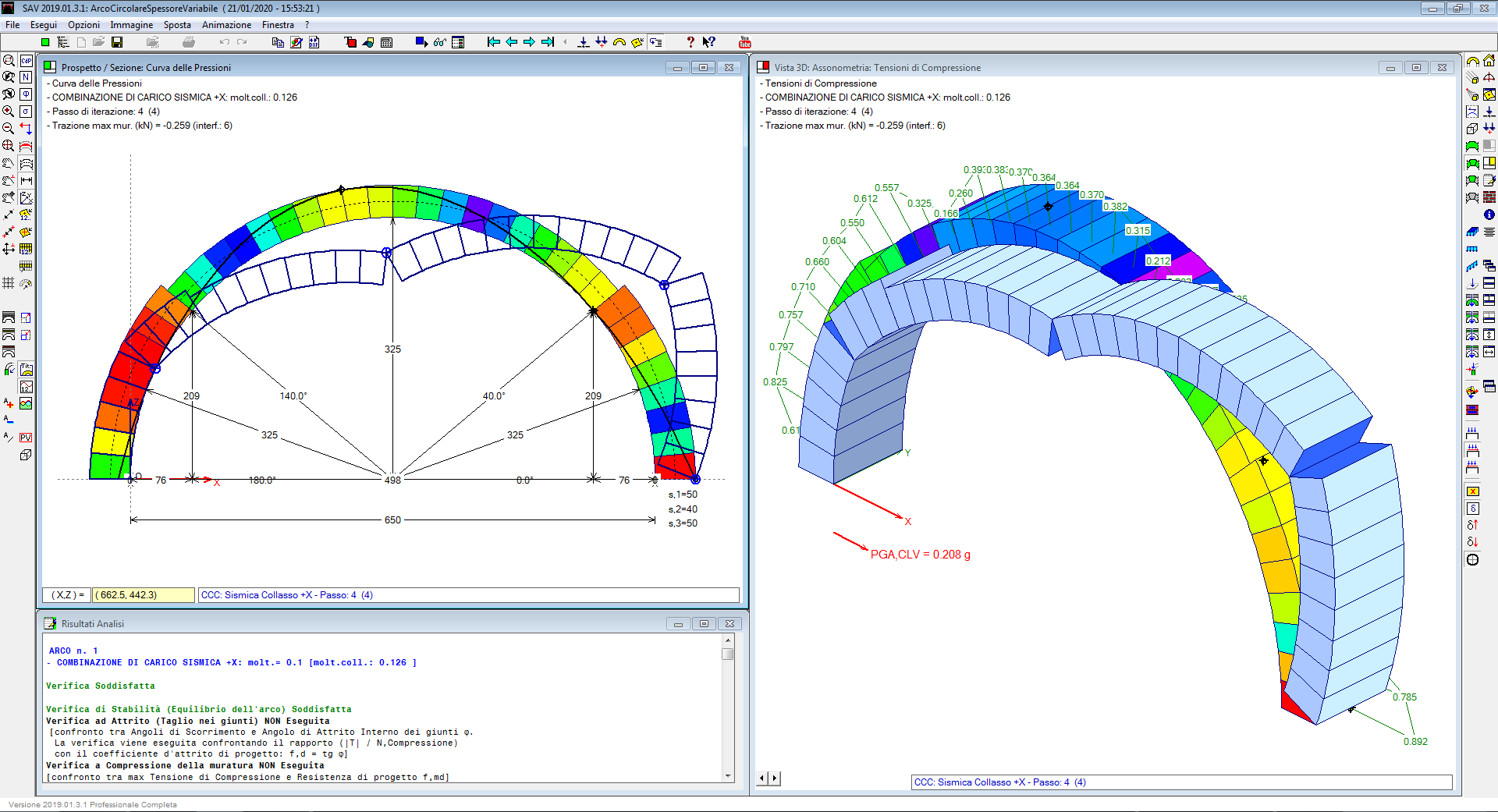
Con riferimento all'esempio illustrato nelle immagini sopra riportate, tutte e tre le verifiche mostrano un determinato valore per il moltiplicatore, da cui si ricava il comportamento maggiormente critico (in questo caso, la verifica ad attrito).
Se lo scorrimento fra i conci fosse stato considerato un comportamento non significativo per questa struttura, la resistenza a compressione sarebbe la causa del limite di sicurezza per il carico verticale. Prescindendo anche dalla verifica a compressione, il limite si sposterebbe ancora più in alto e sarebbe fornito dalla verifica di stabilità, che indica in questo esempio un carico massimo staticamente sostenibile pari a oltre 15 volte il carico in input ad intensità variabile (coincidente con il carico lineare di tipo variabile definito nella CCE 2, mentre il carico lineare di tipo permanente definito nella CCE 1, data la sua natura, resta sempre costante ossia per esso non è attivato il moltiplicatore verticale).
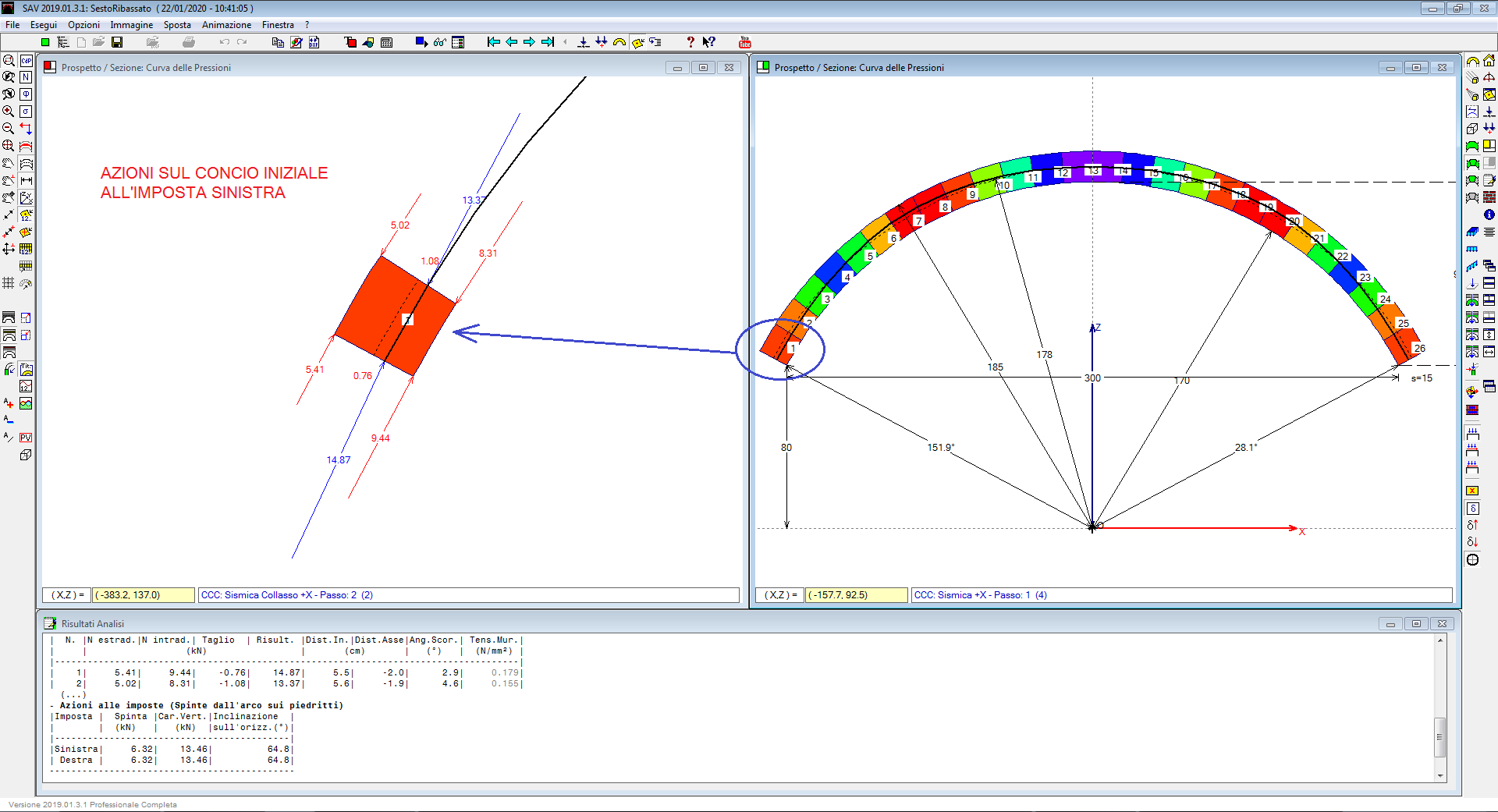
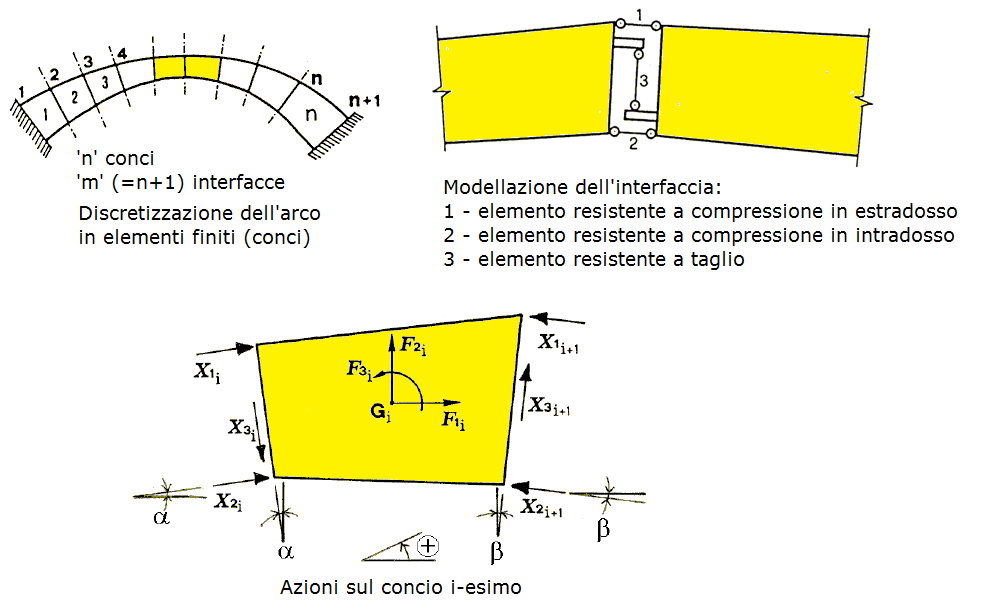
Fra le varie opzioni di post-elaborazione, si segnalano le azioni alle imposte. In figura è riportato l'assetto statico del concio n°1 (concio iniziale a sinistra) per un arco a sesto ribassato.
Le azioni sull’interfaccia sinistra corrispondono alle reazioni dell’imposta sinistra. I valori dei due sforzi normali (intradosso ed estradosso) delle bielle ortogonali all'interfaccia formano insieme lo sforzo normale totale, mentre il taglio è la sollecitazione nella biella parallela all'interfaccia. Sforzo normale e taglio vengono combinati nella risultante, poi scomposta in componente orizzontale (spinta) e verticale.
In accordo con la Normativa vigente (D.M. 14.1.2018, §2.5.3) l'Analisi Sismica, indipendentemente dal numero di Combinazioni di Condizioni di Carico (CCC) definite per l'Analisi Statica, viene eseguita per l'unica Combinazione Sismica, considerando agenti:
(1) i carichi verticali corrispondenti a tutte le Condizioni di Carico Elementari (CCE), affetti dai coefficienti di combinazione ψ2 corrispondenti;
(2) i carichi orizzontali sismici ottenuti dai carichi verticali di tipo gravitazionale applicando un moltiplicatore orizzontale. Tali carichi corrispondono a masse, e sono costituiti dai pesi propri (struttura portante muraria dell'arco, rinfianchi, sottofondo, pavimentazione), e dai carichi aggiuntivi per i quali sia stata selezionata l'opzione relativa al moltiplicatore orizzontale;
(3) eventuali carichi verticali sismici qualora venga considerata la componente sismica verticale. Ai carichi verticali corrispondenti a masse viene attribuita una forza inerziali verticale con moltiplicatore legato al moltiplicatore orizzontale dalle relazioni che, secondo Normativa, correlano le accelerazioni spettrali nelle direzioni orizzontale e verticale;
(4) eventuali carichi orizzontali definiti in input non aventi significato inerziale e quindi con valore indipendente dal moltiplicatore (ad es.: spinte passive dal riempimento).
Il moltiplicatore che traduce i carichi verticali in forze inerziali orizzontali (orientate secondo +X o -X, essendo X la direzione orizzontale del piano dell'arco) viene fatto crescere progressivamente sino a raggiungere la condizione di collasso che segna l'instabilizzazione o la mancata verifica di sicurezza dell'arco. Oltre all'elaborazione della configurazione di collasso, SAV consente l'analisi sotto uno specifico valore in input del moltiplicatore orizzontale.
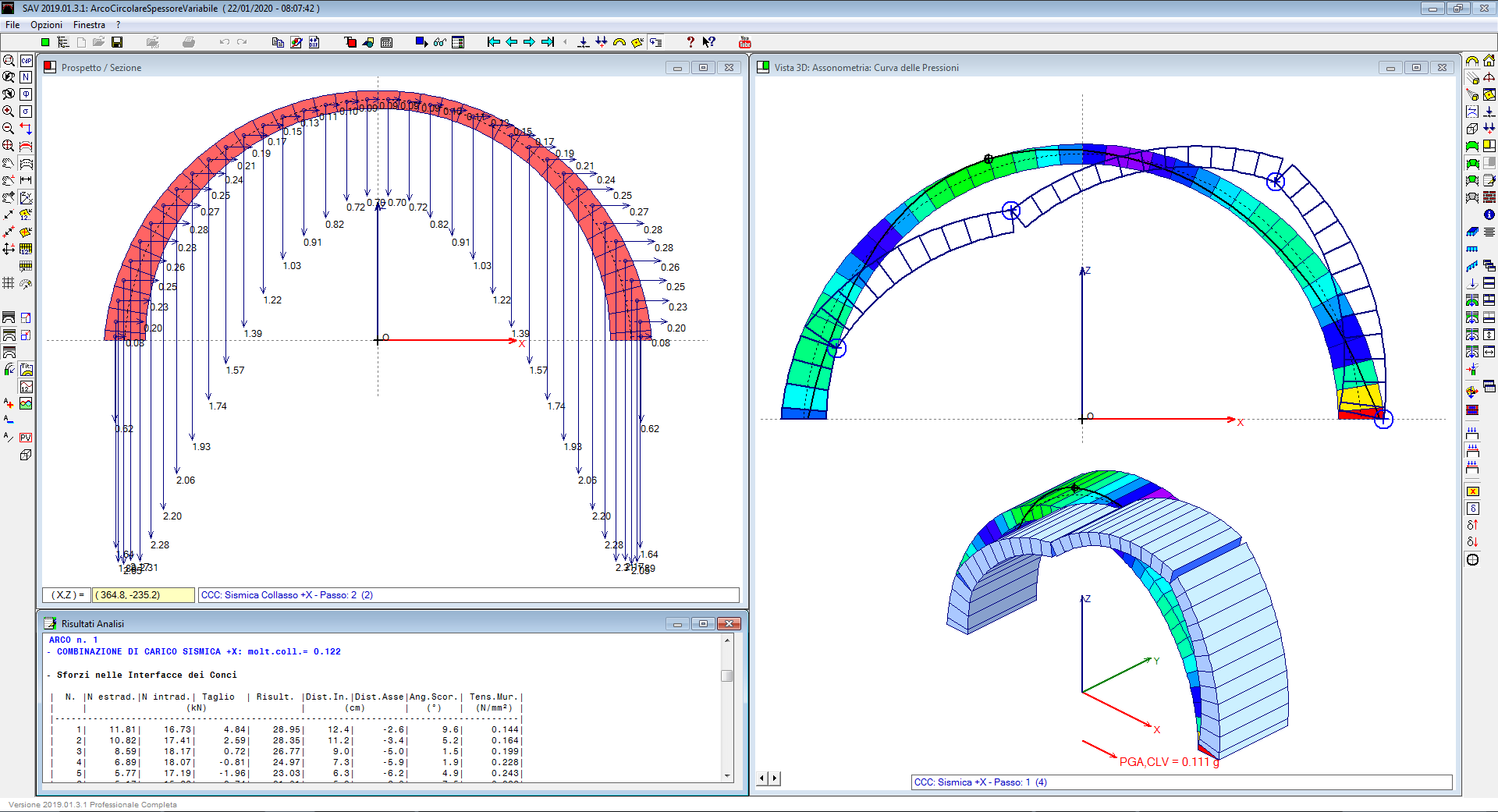
Il moltiplicatore di collasso viene calcolato in base alle verifiche richieste (stabilità ed opzionalmente: attrito, compressione nella muratura, trazione nei rinforzi), per ognuno dei due versi di riferimento (+X e -X) e, nel caso di una volta costituita da più archi, per ogni singolo arco: il minimo fra tutti i valori ottenuti è assunto come moltiplicatore di collasso della struttura voltata. In caso di dissimmetria per geometria o per carichi, il moltiplicatore di collasso risulterà distinto per i due versi +X e -X.
Calcolato il moltiplicatore di collasso, la capacità della struttura in termini di PGA (accelerazione al suolo dell'edificio) allo stato limite SLV (PGA,CLV) viene determinata con riferimento all’analisi dei meccanismi locali di corpo rigido (analisi cinematica), seguendo le specifiche indicazioni normative (Circ. 7 del 21.1.2019, §C8.7.1.2), in relazione anche alla quota in elevazione a cui la struttura è posta.
Secondo la Normativa vigente, l'accelerazione al suolo dipende dal periodo di ritorno TR, a sua volta definito in base al periodo di ritorno dell'azione sismica VR (data da Vita Nominale moltiplicata per il Coefficiente d'Uso) e alla probabilità di superamento PVR (nel periodo VR) corrispondente allo Stato Limite esaminato (SLV). La zona di ubicazione della struttura fornisce i valori di ag in funzione di TR (attraverso i valori per i punti del reticolo di riferimento pubblicati nel testo del D.M. 14.1.2008) e degli altri parametri sismici quali il coefficiente di suolo S (PGA = ag S), ed è così possibile associare al valore di PGA,CLV calcolato da SAV il corrispondente periodo di ritorno TR,CLV, ottenendo in tal modo la capacità in termini di periodo di ritorno.
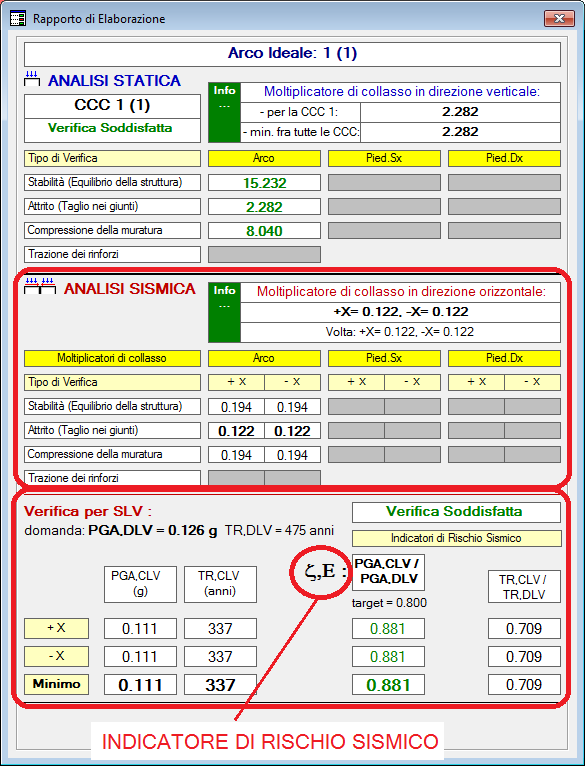
L'Indicatore di Rischio Sismico ζE, consistente nel rapporto tra Capacità e Domanda, costituisce il risultato in sintesi dell'analisi sismica della struttura. La capacità della struttura in termini di PGA (PGA,CLV) o di TR (TR,CLV) indica l'accelerazione (o il corrispondente periodo di ritorno) sostenibili allo stato limite ultimo; la domanda in termini di PGA (PGA,DLV) o di TR (TR,DLV) è l'input sismico. ζE risulta uguale al rapporto (PGA,CLV/PGA,DLV) o (TR,CLV/TR,DLV).
Per un Edificio Esistente sottoposto ad Adeguamento, l'Indicatore di Rischio Sismico in termini di PGA deve essere un valore non inferiore a 0.80 o 1.00, secondo le caratteristiche dell'edificio e del tipo di intervento (D.M. 17.1.2018, §8.4.3); nel caso di miglioramento, il valore target di (zeta)E si ottiene seguendo le indicazioni normative riportate in §8.4.2 e può identificarsi nel valore di 0.6 oppure in un aumento di 0.1 rispetto allo Stato precedente l'intervento.
In ogni caso, ζE caratterizza la capacità antisismica della struttura, e per uno Stato di Progetto a partire dallo Stato Attuale è possibile studiare interventi idonei per l'incremento di questo indicatore (si ricorda che la Normativa, nella Circ. 7 del 21.1.2019, in §C8.3, specifica che il parametro di confronto per l'azione sismica da adottare per ζE è l'accelerazione al suolo agS=PGA).
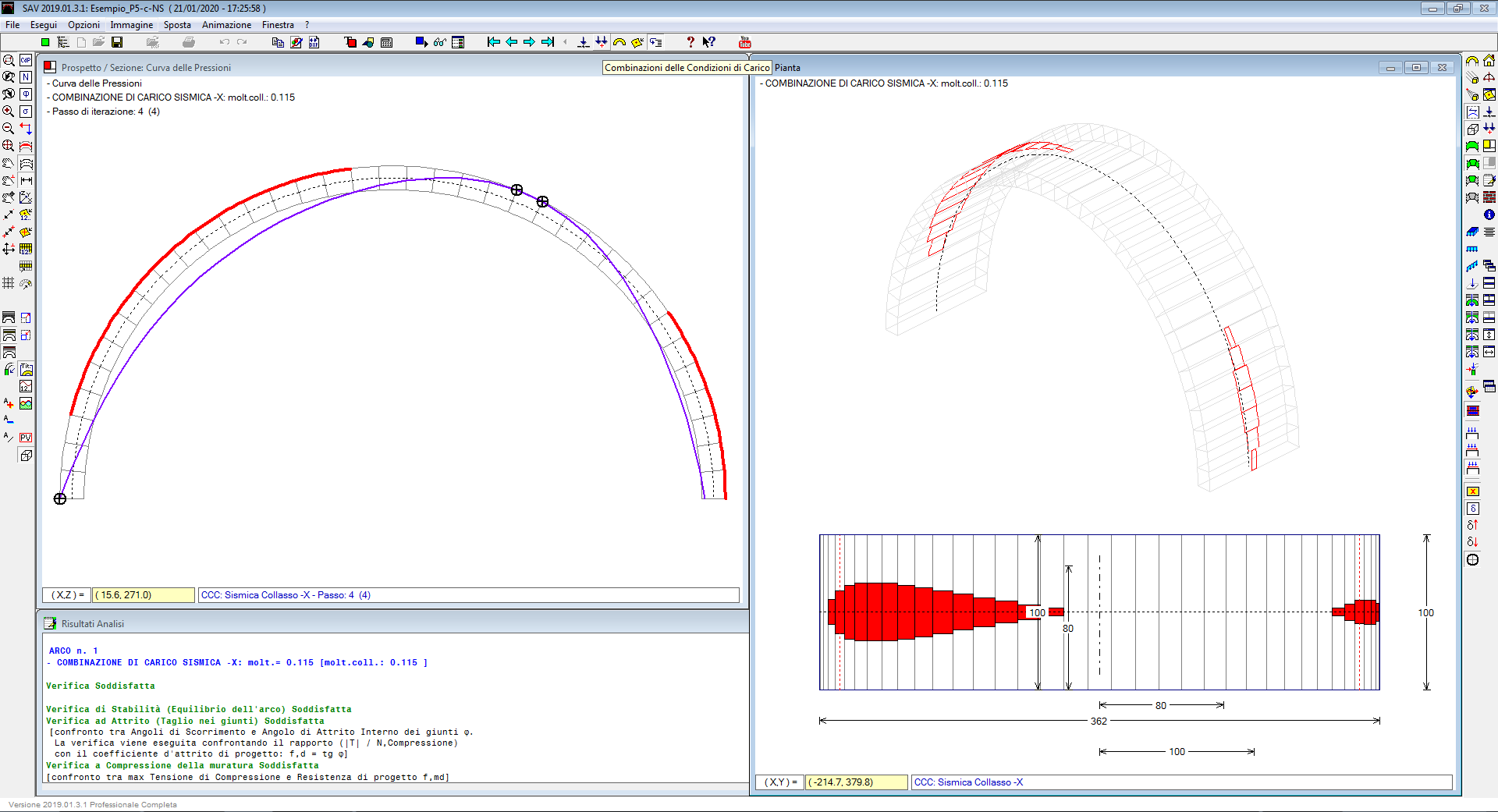
Nell'immagine seguente, il cinematismo di collasso è rappresentato in 2D e in 3D. Le cerniere del meccanismo si formano nelle posizioni determinate dalle forze agenti sui conci, durante il metodo di ricerca di una configurazione stabile ed equilibrata: quando è necessario inserire una quarta cerniera, si attiva il meccanismo, ed è questo il limite del massimo moltiplicatore staticamente ammissibile (o equivalentemente del minimo moltiplicatore cinematicamente ammissibile).
Con riferimento all'esempio illustrato, si osservi che poiché la crisi è determinata dalla verifica ad attrito, il valore del moltiplicatore in questo caso non produce l'immediata formazione del cinematismo ma si tradurrà fisicamente in una rottura per scorrimento tra conci. Il cinematismo rappresentato in figura si riferirà allo stato raggiungibile per effetto delle sole crisi di stabilità.
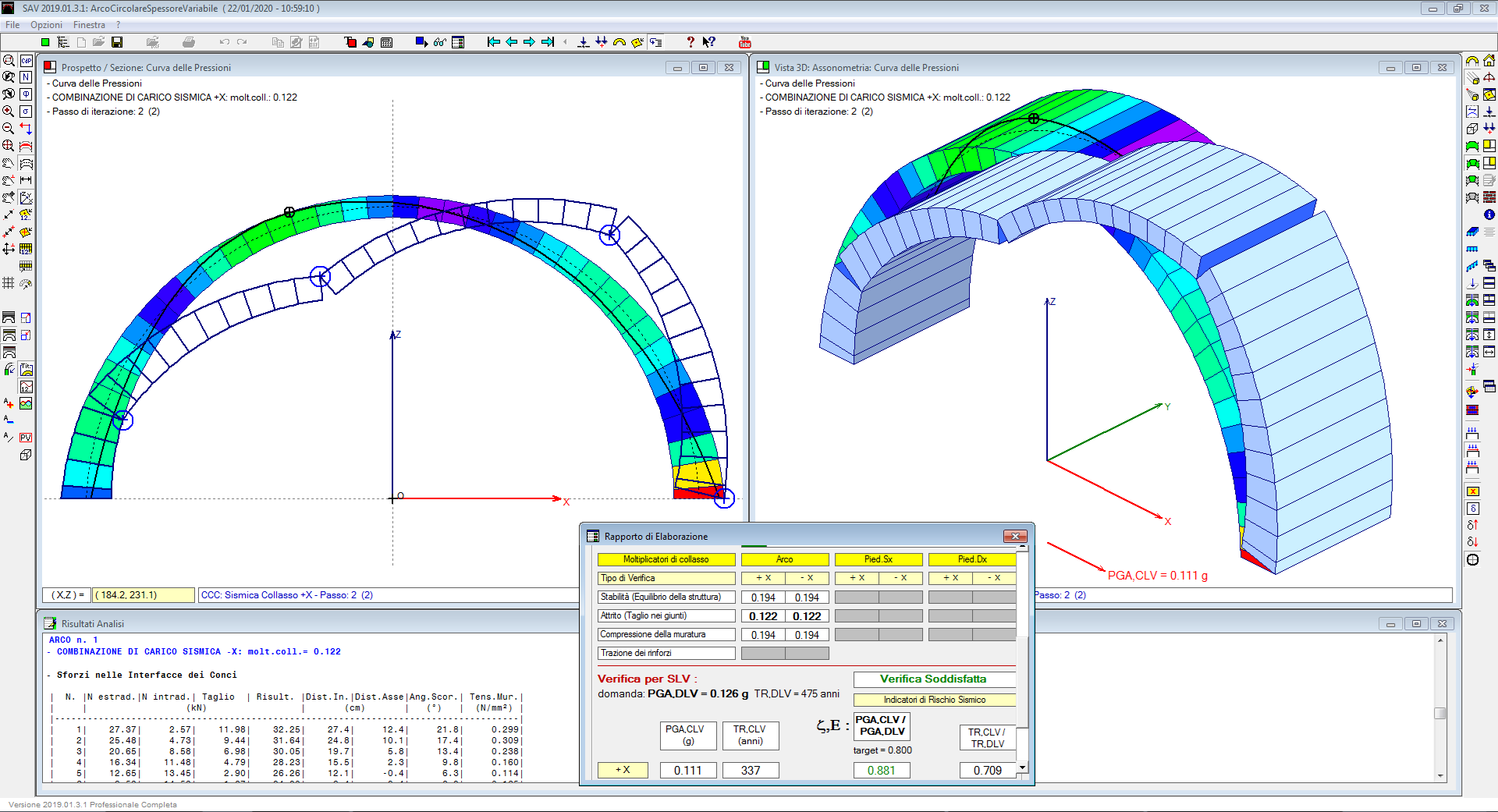
Può quindi essere interessante esaminare la formazione del cinematismo facendo riferimento alla sola verifica di stabilità: ciò illustra in modo efficace il procedimento di calcolo iterativo.
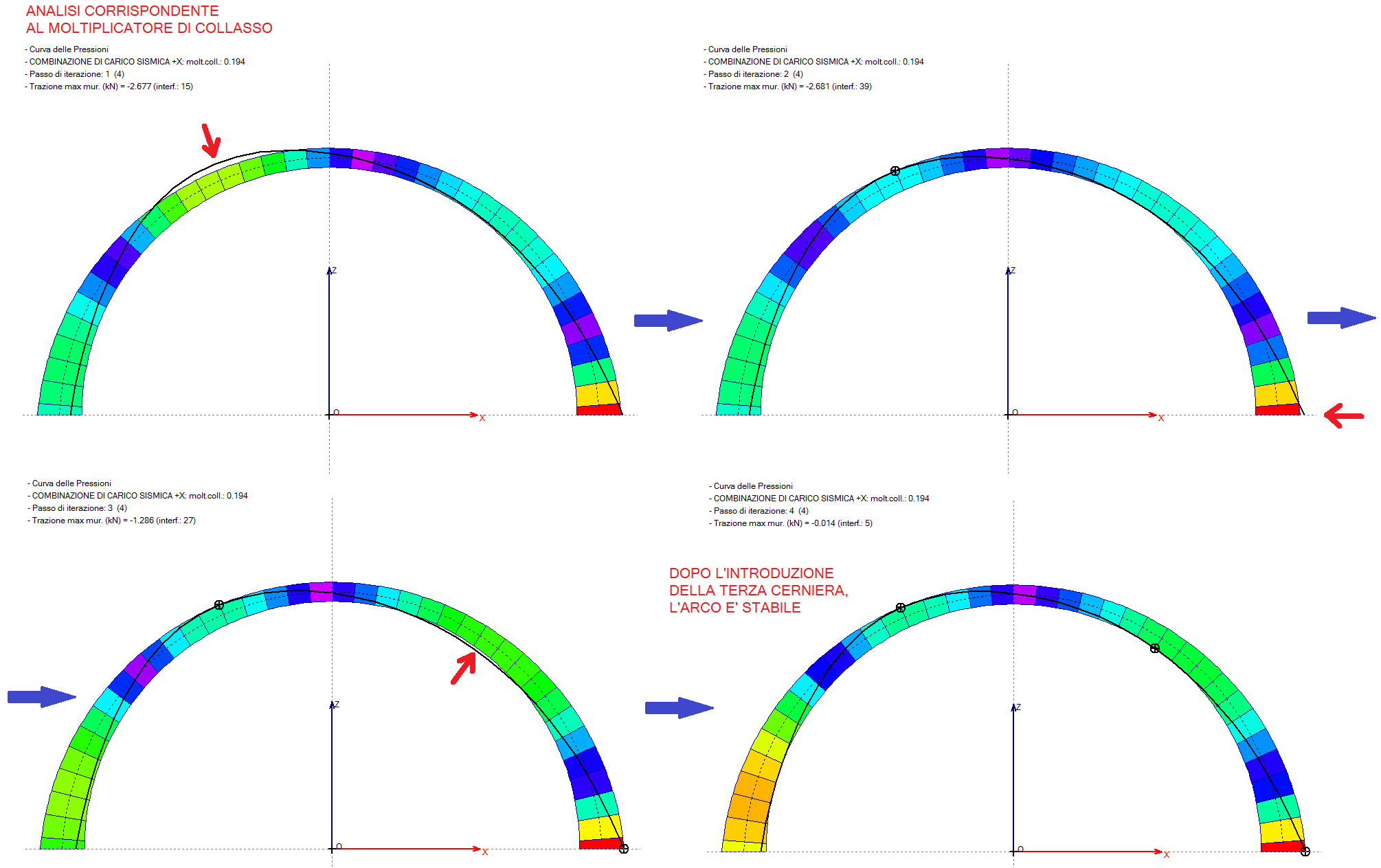
Nell'immagine soprastante, l'arco sottoposto all'incremento progressivo del moltiplicatore, in corrispondenza del valore di questo pari a 0.194 raggiunge l'equilibrio con 4 iterazioni, corrispondenti a 3 cerniere. Ad ogni passo, il procedimento compensa la maggiore trazione rilevata, puntando a far rientrare la curva delle pressioni entro la sagoma dell'arco.
Con un moltiplicatore più grande, la soluzione trovata non sarebbe più accettabile: anche dopo la terza cerniera, la curva delle pressioni fuoriuscirebbe in una sezione e quindi non potrebbe garantire l'equilibrio.
Le applicazioni dell'analisi con cedimenti delle imposte sono varie, di tipo sia statico che sismico.
Cedimenti verticali possono manifestarsi a causa di movimenti nel terreno di fondazione; cedimenti orizzontali differenziali fra le imposte caratterizzano il comportamento dinamico sismico delle strutture e possono determinare instabilizzazione degli archi (si pensi ad esempio alle volte sottili su ampia luce).
La variazione delle spinte sulle imposte, indotta dalla deformazione dell'arco, può assumere un ruolo fondamentale nella sollecitazione di ribaltamento fuori piano di pareti murarie su cui la struttura voltata è impostata.
I cedimenti possono essere di tipo traslazionale, orizzontali e/o verticali, e/o di tipo rotazionale, in entrambi i versi; fra i casi più interessanti: il cedimento orizzontale verso l'esterno (per 'cedimento' si intende quindi in tal caso lo spostamento orizzontale) che può essere contemporaneo e asincrono per le due imposte (ad es. entrambi gli spostamenti orizzontali verso l'esterno), ed il verticale verso il basso (in tal caso il cedimento consiste nella traslazione verticale delle imposte).
L'analisi dei cedimenti, preventiva all'elaborazione di calcolo della struttura e condotta per la combinazione di carico statica, esamina la formazione delle tre cerniere che, a seguito del cedimento in input, rendono isostatico l'arco. Sulla configurazione isostatica dell'arco verrà poi eseguita l'elaborazione di calcolo statica e sismica.
La procedura di analisi limite in caso di cedimenti alle imposte oltre ai carichi applicati richiede alcune specifiche considerazioni.
Per soli carichi esterni le incognite cinematiche, in condizioni di equilibrio, risultano ovunque nulle e quindi l'analisi della stabilità si limita al controllo della compatibilità tra la sagoma iniziale dell'arco e la curva delle pressioni.
Nel caso di compresenza di cedimenti vincolari, tale controllo di compatibilità deve essere effettuato tra la curva delle pressioni e la configurazione variata dell'arco, funzione di incognite cinematiche (le rotazioni nelle cerniere) che dipendono sia dai cedimenti stessi sia dai carichi applicati.
Si consideri dunque un arco sottoposto ad una condizione di carico verticale, per la quale la struttura risulti "stabile", e ad una configurazione di cedimenti anelastici dei vincoli, che per semplicità si possono pensare concentrati nelle imposte.
Per effetto del cedimento (consistente in uno o più movimenti fra traslazione orizzontale, traslazione verticale e rotazione, ad una o ad entrambe le imposte) la struttura si trasforma da una configurazione tre volte iperstatica ad una isostatica: di conseguenza la curva delle pressioni diventa tangente in tre punti alla sagoma dell'arco. Si formano 3 cerniere delle quali si deve individuare la posizione.
La figura seguente illustra le condizioni statiche e cinematiche che vengono controllate per la soluzione strutturale dell'arco: la configurazione che rispetta l'equilibrio deve assicurare sia l'assenza di trazioni con annullamento delle forze nelle bielle ortogonali all'interfaccia che risultano tese [(a); le forze X1i e X2i si riferiscono alle bielle d'interfaccia] , sia l'assenza di ogni compenetrazione di materiale nella direzione delle bielle ortogonali all'interfaccia interessate dalla forza di compressione (b).
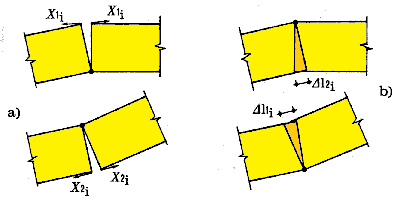
L'algoritmo risolutivo è il seguente.
Fase 1. Dati in input: arco, carichi statici esterni, cedimenti alle imposte.
Fase 2. Si individuano tutte le triplette di cerniere in grado di rispettare le condizioni richieste dal punto di vista cinematico (assenza di compenetrazione di materiale murario in corrispondenza delle bielle compresse). Se non esiste alcuna tripletta che rispetta la condizione cinematica, i cedimenti definiti in input non sono ammissibili e determinano un'impossibilità di equilibrio.
Fase 3. Fra tutte le triplette di cerniere individuate nella fase 2 si ricerca la tripletta in grado di soddisfare l'equilibrio con curva delle pressioni interna alla sagoma (e passante per le cerniere determinate dai cedimenti), facendo riferimento all'arco deformato. Se non esiste alcuna tripletta con tale proprietà, i carichi definiti in input non sono ammissibili e determinano un'impossibilità di equilibrio.
Se invece la tripletta che soddisfa le condizioni cinematiche e statiche viene individuata, si assegnano all'arco le 3 cerniere che lo degradano da iperstatico a isostatico.
Fase 4. Sulla configurazione originaria dell'arco, modificata dall'inserimento delle 3 cerniere, è possibile condurre una normale analisi per il calcolo di un moltiplicatore statico (relativo a carichi verticali variabili) o sismico (relativo all'intensità delle forze sismiche); tale procedura è da considerarsi significativa nel caso di cedimenti di piccola entità rispetto alle dimensioni geometriche dell'arco. Come per ogni altra analisi condotta con l'algoritmo implementato in SAV, il moltiplicatore viene fissato dalla formazione della quarta cerniera oppure da una condizione non ammissibile (ad esempio, sforzo normale risultante di trazione in una interfaccia non soggetta a rinforzo); ad ogni passo dell'analisi viene in ogni caso effettuata una verifica sul residuo non equilibrato: quando questo risulta non nullo, l'equilibrio non è più assicurato.
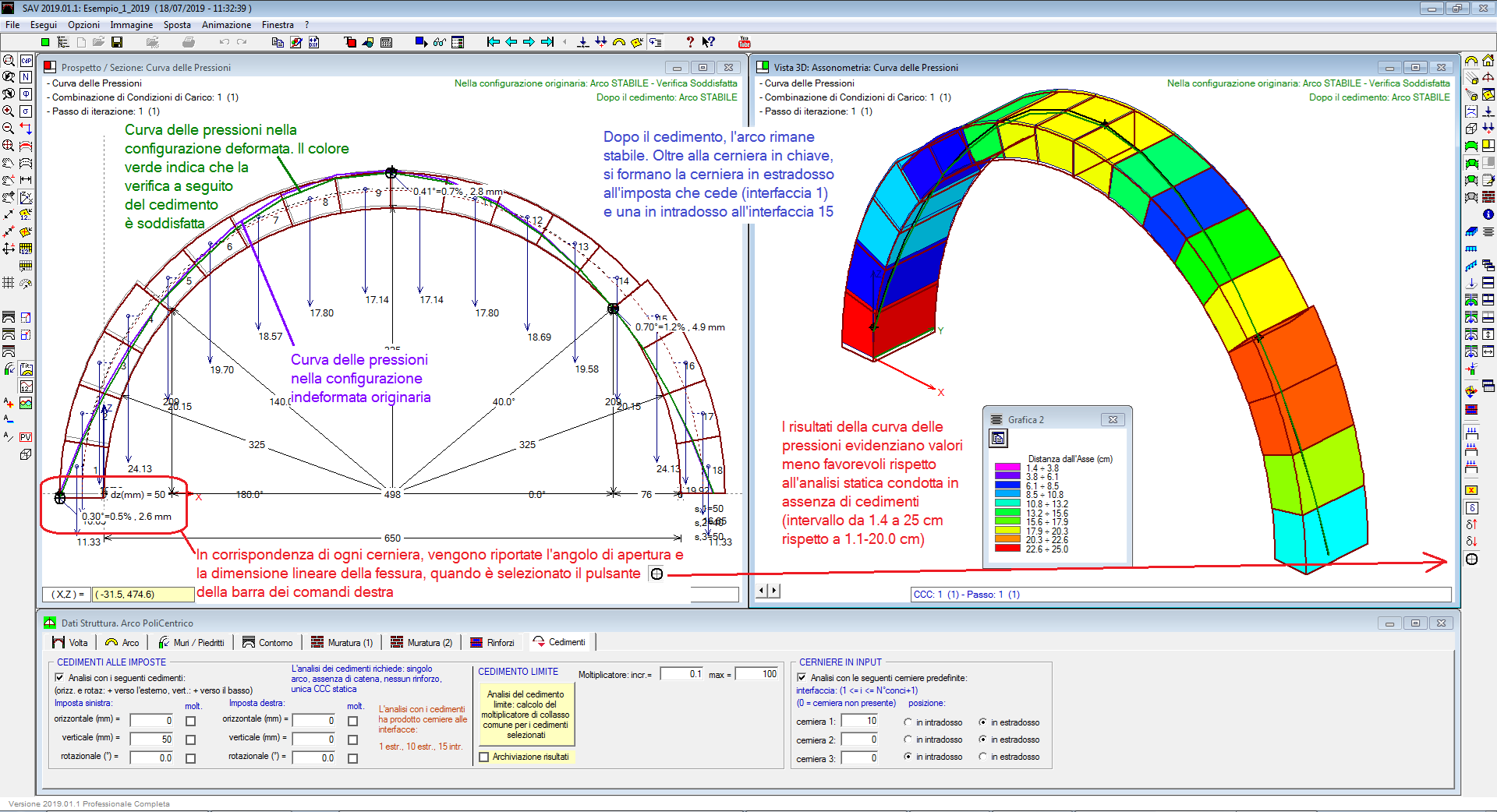
Analisi del cedimento limite. Nel caso che il cedimento applicato non sia di piccola entità, è necessario esaminare l'equilibrio dell'arco nella configurazione geometrica variata. Questa procedura viene seguita nel corso dell'analisi del cedimento limite, quando, sottoponendo il cedimento ad un moltiplicatore crescente, viene ricercato il valore massimo del moltiplicatore (moltiplicatore di collasso) per il quale l'arco deformato non è più in equilibrio rispettando la curva delle pressioni interna alla geometria deformata dell'arco stesso.
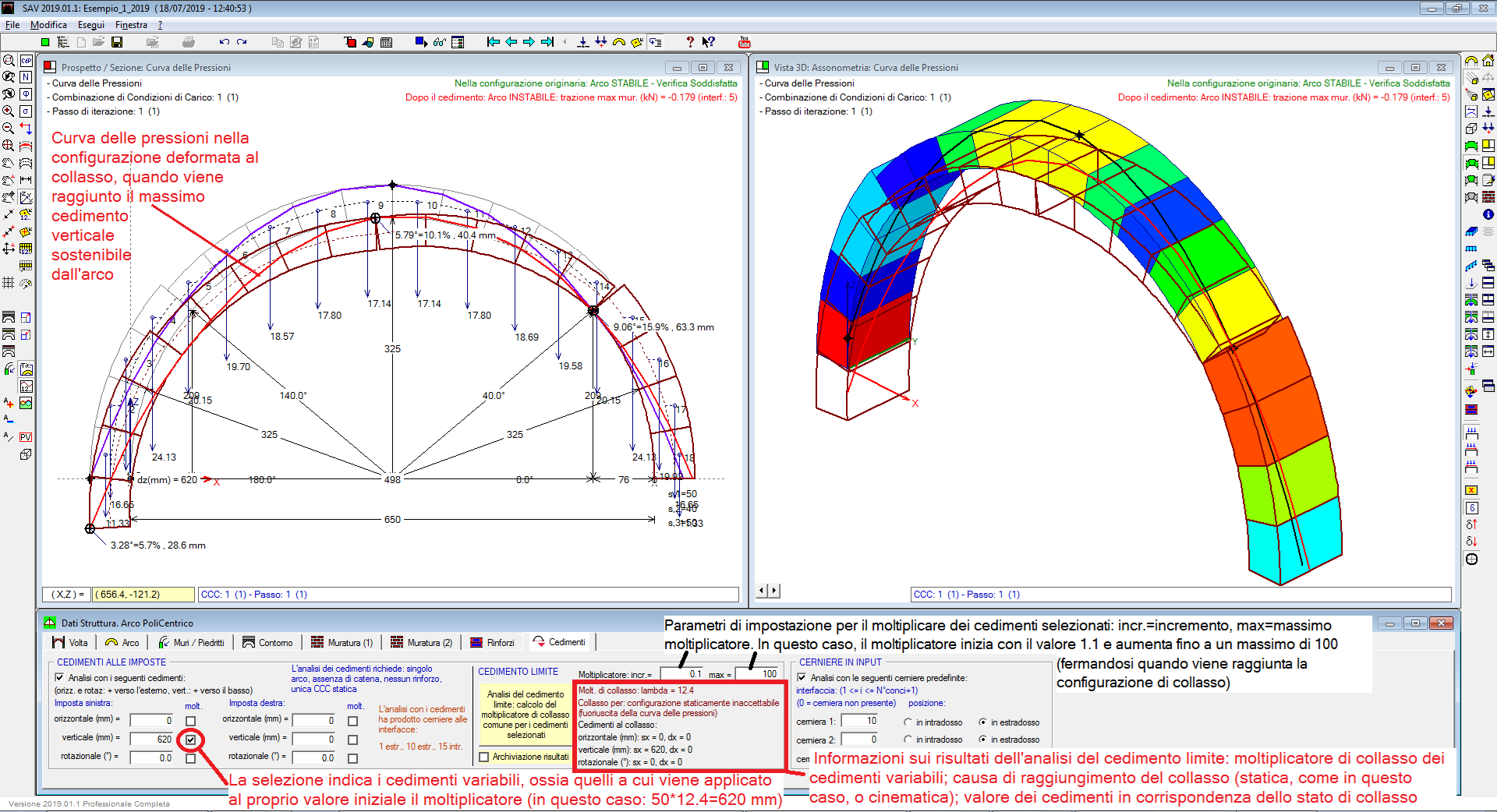
La determinazione del cedimento limite trova un'importante applicazione nell'analisi sismica.
Gli effetti sismici sull'arco possono infatti essere correlati non tanto alle forze inerziali orizzontali agenti sull'arco stesso, ma alle sollecitazioni e deformazioni sismiche delle strutture su cui l'arco si imposta.
Ad esempio, cedimenti che rappresentano una traslazione orizzontale delle imposte asincrona (allontanamento o avvicinamento reciproco contemporaneo) possono essere considerati rappresentativi di effetti sismici trasmessi all'arco dalle deformazioni delle strutture sulle quali l'arco si imposta.
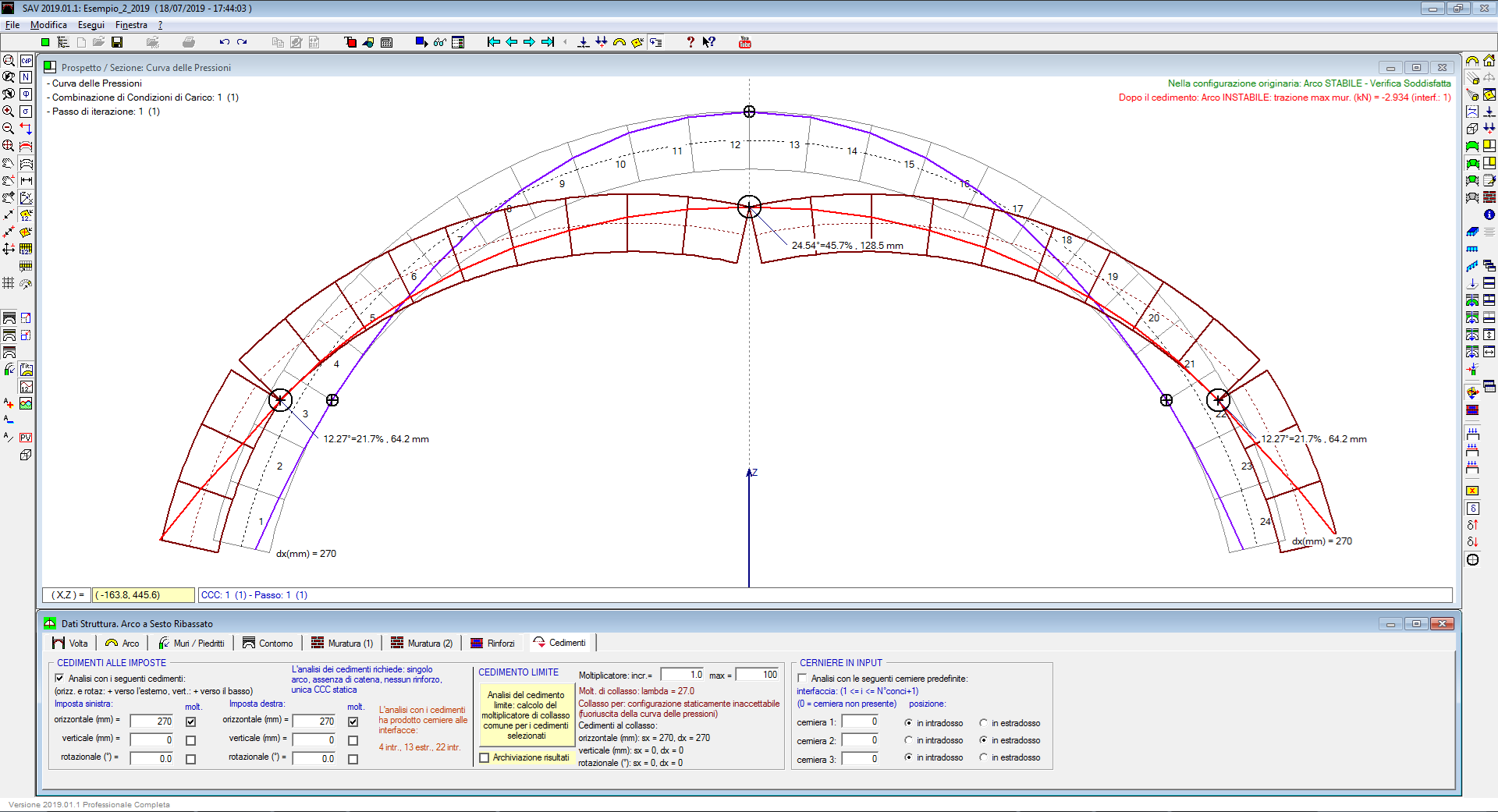
Infatti, le pareti murarie dell'organismo edilizio da cui l'arco spicca possono vibrare in modo asincrono: si pensi ad esempio ad un arco impostato da una parte su una parete perimetrale e dall'altra su una parete interna. Le pareti interne sono maggiormente connesse all'organismo murario dell'edificio, e la vibrazione delle imposte dell'arco può avvenire in modo asincrono. L'allontanamento reciproco delle imposte può determinare una deformazione della volta tale da provocarne il crollo, specialmente in caso di volte sottili (meccanismi riscontrati ad esempio nei recenti eventi sismici dell'Italia Centrale).
In tali casi l'analisi sismica dell'arco può svolgersi analizzando gli effetti inerziali non tanto sulle masse dell'arco stesso (studio dell'arco indeformato sottoposto a forze orizzontali crescenti), ma piuttosto sulle strutture che lo sostengono con conseguenti possibili movimenti asincroni delle imposte, valutandone gli effetti sulla stabilità dell'arco.
Specifiche funzionalità consentono il riesame di tutto il processo incrementale, in modo tale che, qualora si voglia fissare un limite alla fessurazione o all'angolo di apertura delle cerniere, si possa agevolmente identificare il moltiplicatore della corrispondente configurazione, individuando il valore del massimo cedimento ammissibile.
Supponiamo, per l'esempio in figura seguente, che si consideri accettabile una fessurazione non oltre 30 mm.: riesaminando il percorso fessurativo progressivo, è possibile individuare il corrispondente cedimento verticale, da assumere come cedimento limite effettivo.
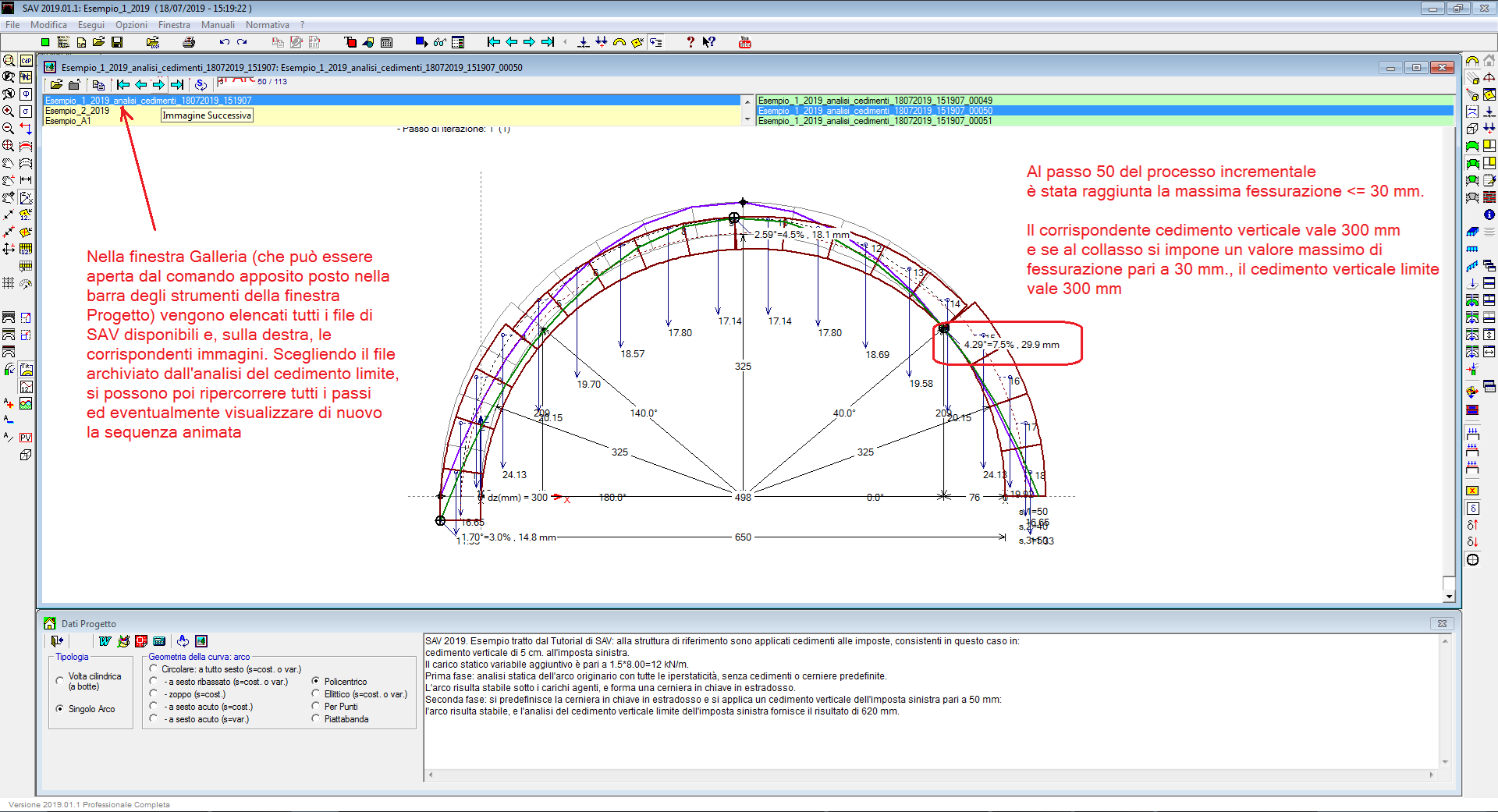
A partire dalla versione 2021, SAV gestisce l'analisi di ponti esistenti in muratura, di tipo stradale o ferroviario, conformemente alla Normativa vigente: D.M. 17.1.2018 e Circolare 7 del 21.1.2019, linee guida CNR-DT 213/2015: "Istruzioni per la Valutazione della Sicurezza Strutturale di Ponti Stradali in Muratura", normative specifiche per i ponti ferroviari.
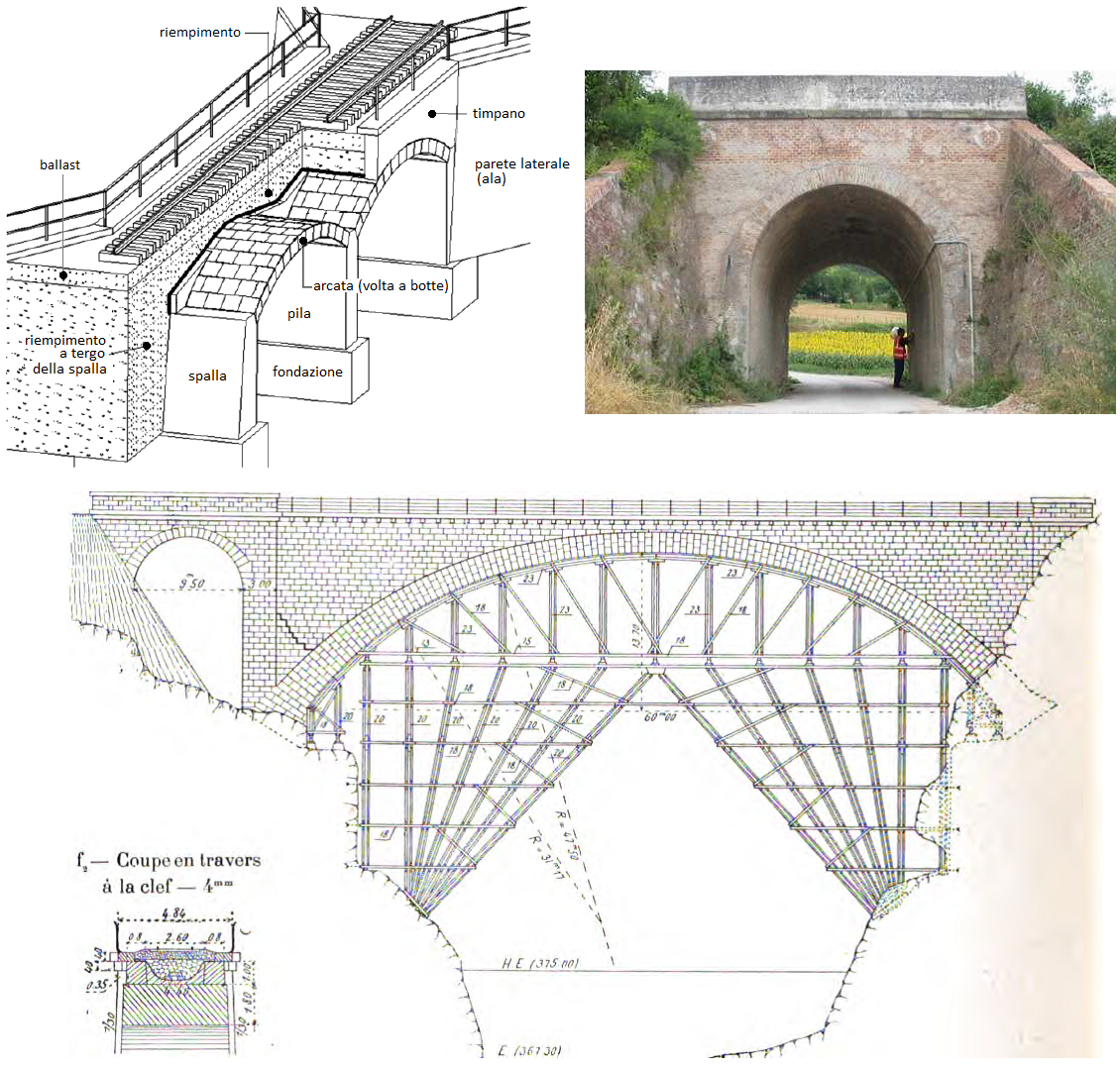
I ponti possono essere monocampata o multicampata. Nei ponti monocampata entrambi i piedritti sono costituiti dalle spalle, soggette alle spinte del terreno, calcolate automaticamente dal software ed assegnate come azioni lungo lo sviluppo in elevazione dei piedritti.
SAV distingue i casi di spalle tozze o snelle, trattate diversamente dal punto di vista delle spinte. La spinta statica si distingue fra spinta a riposo e spinta attiva, mentre la spinta passiva può essere considerata in percentuale selezionabile in input: ciò permette di inquadrare l'effettiva quota-parte di spinta passiva che può essere mobilitata per l'equilibrio della struttura. L'incremento di spinta del terreno dovuto all'azione sismica viene distinto fra i casi di spalla snella (metodo di Mononobe-Okabe) o tozza (metodo di Wood).
La verifica di conformità alla regola d'arte (§4.3 CNR-DT 213/2015) propone le formule di riferimento ed il calcolo del fattore di difformità: si tratta di una funzionalità molto importante, in quanto determina il valore di progetto del Fattore di Confidenza e, di conseguenza, l'esito delle verifiche di resistenza.
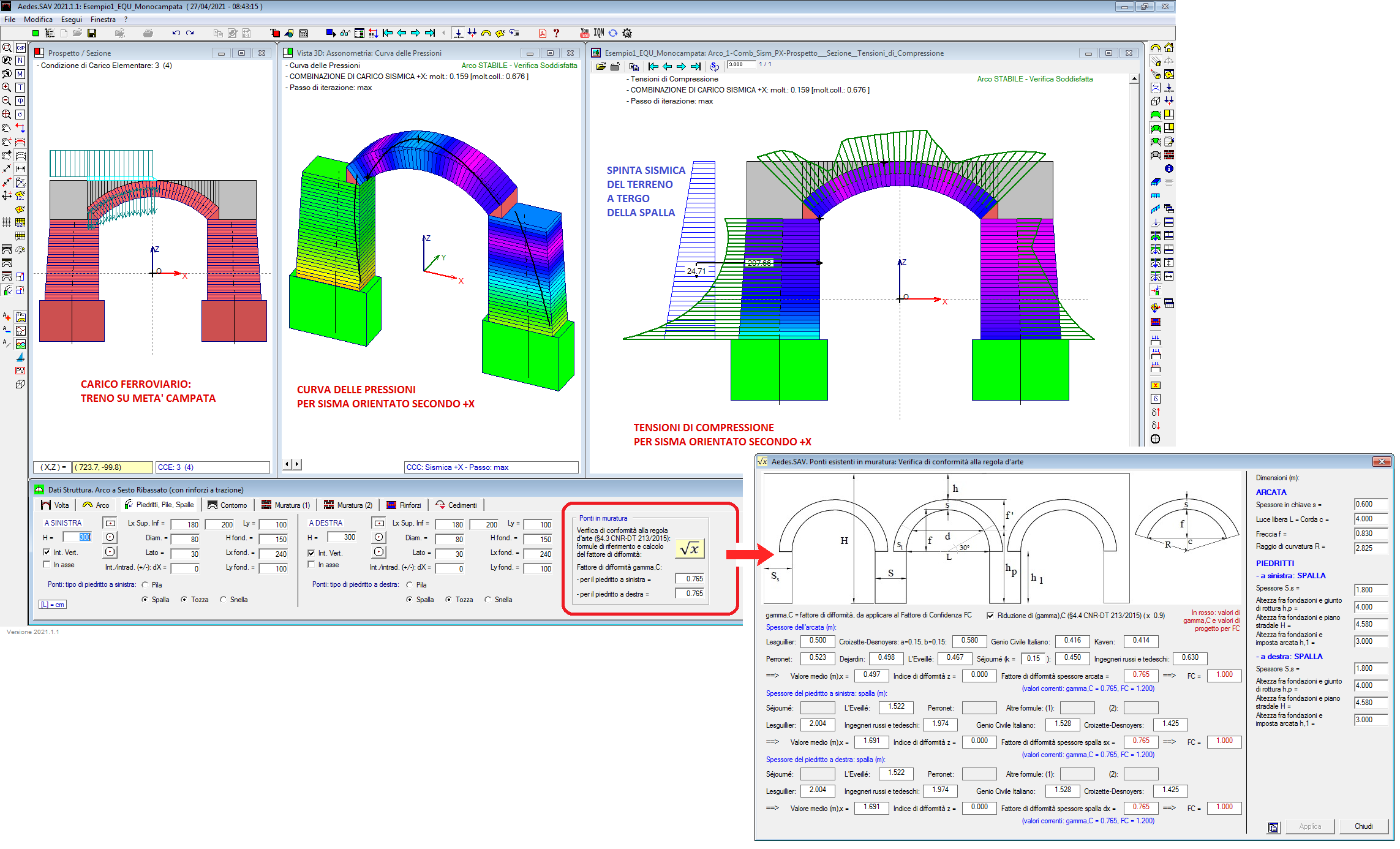
Attraverso un approfondimento basato sugli studi del Prof. Massimo Corradi (Empirical methods for the construction of masonry arch bridges in the 19th century), le relazioni empiriche proposte dalle Linee guida del CNR sono state verificate e implementate in SAV in una finestra dedicata.
Viene considerato inoltre il possibile stato di degrado delle strutture attraverso l'apposito fattore di riduzione delle resistenze.
Per i ponti multicampata, opportune funzionalità consentono lo scambio delle forze di interazione fra le imposte delle arcate adiacenti ed i piedritti, operando su più modelli: gli esempi applicativi del software illustrano la procedura di calcolo in grado di definire il moltiplicatore di collasso tenendo conto di più campate e dei loro differenti stati di carico.
Le risultanti e le tensioni alla base delle spalle e delle pile consentono la verifica delle strutture di fondazione.
Per quanto riguarda i carichi, SAV consente la definizione diretta dei carichi da ponti stradali e ferroviari, in accordo con la Normativa vigente (D.M. 17.1.2018); i carichi possono tuttavia essere definiti secondo altri criteri (ad esempio, per i ponti ferroviari: carichi da treno reale).
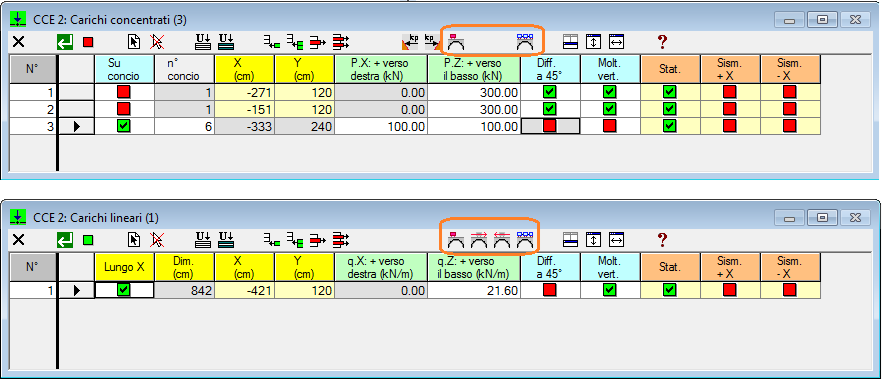
In figura seguente, un estratto da §5.1.3.3.5 del D.M. 17.1.2018. L'immagine indica i tipi di carico per ponte stradale.
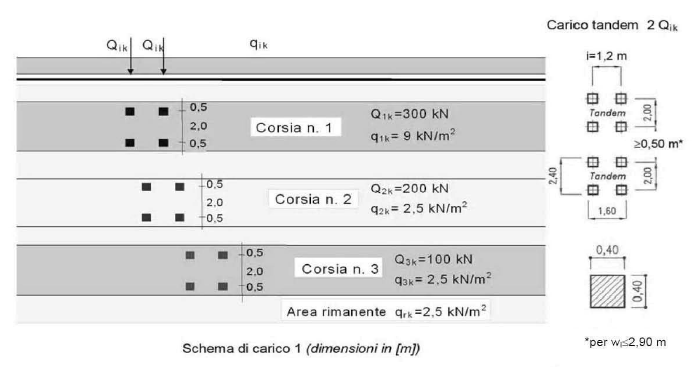
La definizione del carico stradale richiede una volta muraria di profondità almeno 240 cm. La coppia di carichi concentrati viene predisposta, dal comando di SAV, in posizione eccentrica a 1/4 della luce dell'arco, posizione che si ritiene possa generare i massimi effetti (i dati in input consentono comunque lo spostamento del carico in altre posizioni, e questo può essere applicato nello stesso file di SAV definendo più condizioni di carico elementari CCE, ognuna con i carichi in una certa posizione, considerate ovviamente non contemporanee fra loro nelle combinazioni delle condizioni CCC).
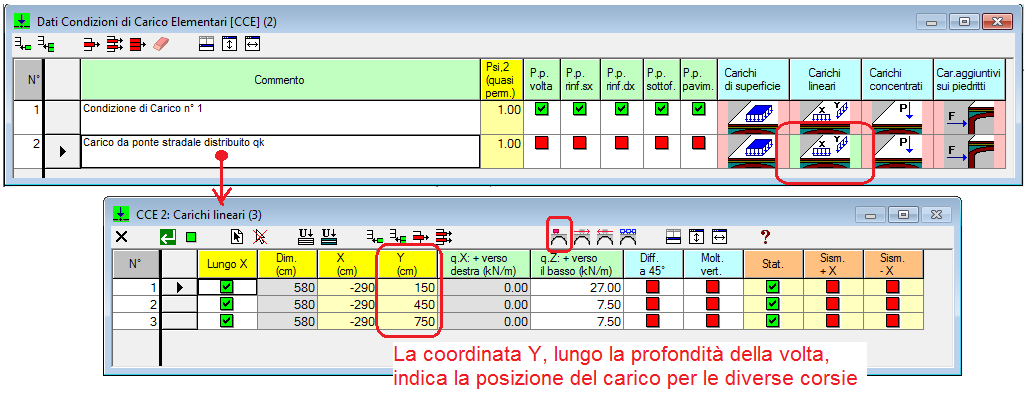
Seguendo lo schema normativo della Tab. 5.1.II del D.M. 17.1.2018, nel caso in cui la volta abbia profondità maggiore di 3.00 m, le coppie di carichi concentrati vengono applicati in numero non superiore a 3 in corrispondenza delle corsie, ognuna di 3.00 m, in cui la volta viene suddivisa, con valori decrescenti: 300 kN nella prima corsia, 200 kN nella seconda, 100 kN nella terza.
Il carico distribuito, definito come carico di superficie, viene ricondotto a carico lineare moltiplicando per la larghezza della corsia. Anche per il carico distribuito viene considerata la suddivisione in corsie, in base alla profondità della volta, ed il valore del carico lineare è di 27.00 kN/m per la prima corsia e di 7.50 kN/m per tutte le altre.
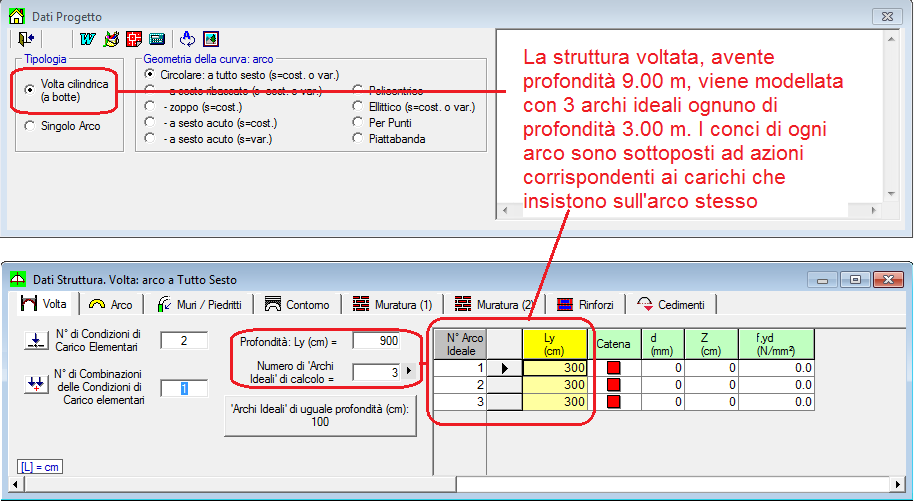
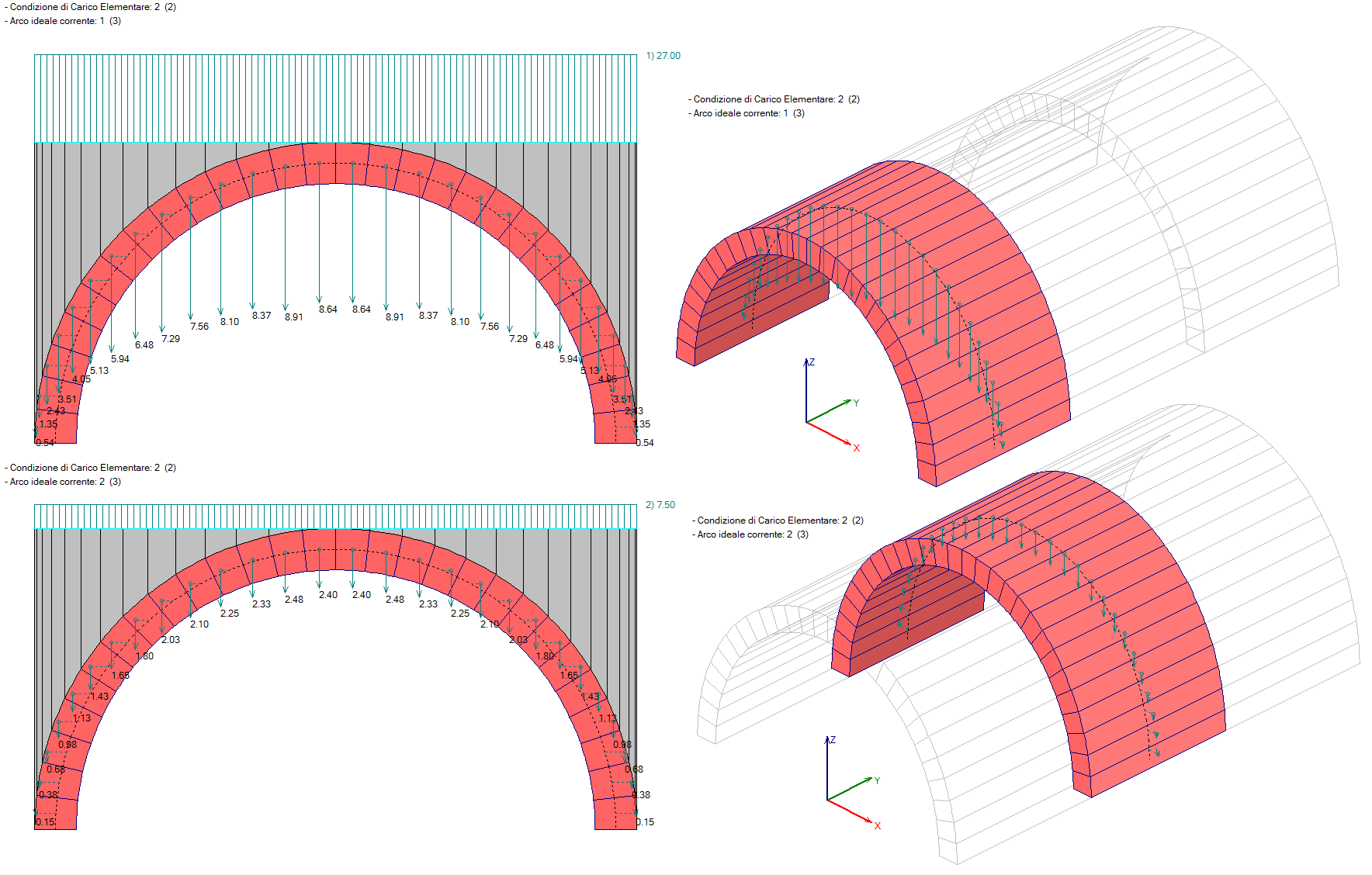
SAV consente la suddivisione di una volta in archi ideali: se quindi la volta ha profondità maggiore di 3.00 m, è possibile suddividerla in archi ognuno con profondità <=3.00 m. corrispondente alla larghezza della corsia, in modo che i carichi stradali definiti per ogni corsia si trasformino in azioni sui conci dell'arco ideale corrispondente alla corsia. Se la struttura voltata non viene suddivisa in più archi ideali, ma coincide con l'unico arco che la definisce, le azioni nei propri conci saranno la risultante di tutti i carichi definiti.
Può essere preferibile la modellazione in archi ideali corrispondenti alle corsie, in quanto gli effetti dei carichi, variabili da una corsia all'altra, sono in tal modo relazionati alla zona del ponte dove insistono.
Nelle figure seguenti, la struttura voltata di un ponte stradale, di profondità 9.00 m, viene suddivisa in 3 archi ideali con profondità corrispondenti alla larghezza delle corsie (3.00 m). Vengono mostrati i carichi distribuiti da ponte stradale nel primo arco (prima corsia) e negli altri archi (corsie successive).
SAV consente anche la modellazione dell'azione di frenamento dei carichi stradali, così come definita in §5.1.3.5 del D.M. 17.1.2018. L'azione orizzontale va considerata applicata a livello della pavimentazione e viene assunta uniformemente distribuita, e le forze orizzontali vengono trasferiti ai conci.
Nella manualistica di SAV si propongono approfondimenti riguardanti le categorie EQU e STR dello stato limite ultimo per la verifica di sicurezza del ponte stradale esistente in muratura, secondo le indicazioni del documento CNR-DT 213/2015: "Istruzioni per la Valutazione della Sicurezza Strutturale di Ponti Stradali in Muratura".
Per quanto riguarda i carichi su ponti ferroviari, nel caso dei carichi distribuiti un apposito comando permette la scelta del tipo di carico in base a quanto indicato dalla Normativa (figura seguente)
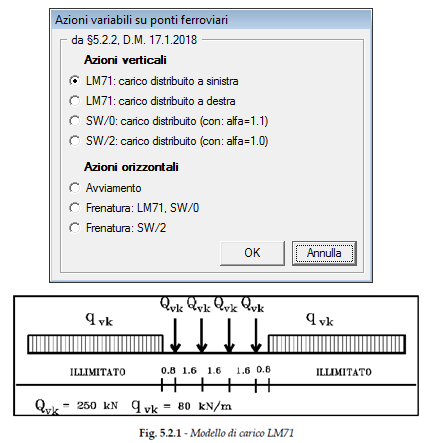
Per la definizione del carico distribuito qvk (a sinistra o a destra) relativo allo schema LM71, il comando automatico di SAV controlla che la luce sia superiore a 480 cm, a causa del posizionamento dei 4 carichi concentrati Qvk; la definizione dei carichi concentrati stessi richiede una luce > 480 cm. Per i modelli di carico SW è richiesta una luce superiore a 530 cm per SW/0 e 700 cm. per SW/2. Le azioni orizzontali di avviamento e frenatura corrispondono alle indicazioni di §5.2.2.3.3 D.M. 17.1.2018.
Per tutti i carichi concentrati e distribuiti su ponti stradali e ferroviari è possibile modificare i valori e le posizioni impostate dai comandi automatici di SAV; in ogni caso, la gestione dei carichi verticali e orizzontali in input consente la modellazione di configurazioni di carico personalizzate.
Per i ponti esistenti in muratura l'interazione con le spinte passive dal riempimento (reazioni passive riguardanti non il terreno, ma il materiale di riempimento che insiste sopra l'arcata) può assumere importanza notevole, particolarmente nel caso delle arcate a tutto sesto: a questo argomento sono dedicati approfondimenti nella manualistica di SAV.
E' possibile eseguire l'analisi dell'arco considerando anche la componente sismica verticale.
Le forze corrispondenti possono riferirsi al 100% oppure al 30% degli effetti, con forze disposte verso l'altro, verso il basso oppure dipendenti dal cinematismo. La selezione delle opzioni viene effettuata nella finestra dei Parametri di Calcolo.
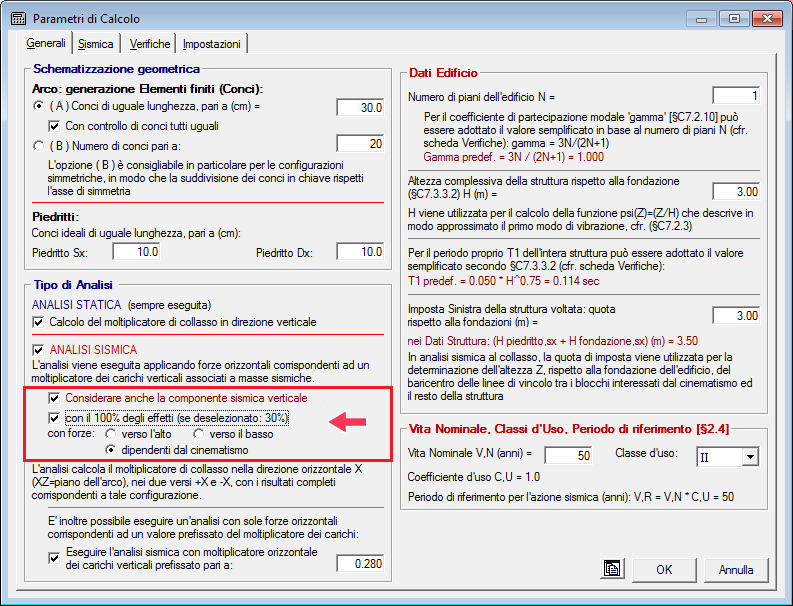
La scelta sulla riduzione degli effetti del sisma verticale secondo la percentuale del 30% corrisponde alle indicazioni date in §7.3.5 NTC18, secondo cui per un sistema piano (posto per ipotesi nel piano XZ) quale l'arco analizzato in SAV, la risposta sismica è calcolata unitariamente per le due componenti X e Z applicando l'espressione: 1.00 · EX + 0.30 · EZ
dove gli effetti più gravosi si ricavano dal confronto tra le due combinazioni ottenute permutando circolarmente i coefficienti moltiplicativi 1.00 e 0.30.
Si considera tuttavia la possibilità che, a favore di sicurezza, la componente sismica verticale non venga ridotta, tenendo conto del fatto che le strutture voltate sono particolarmente sensibili alle variazioni delle forze verticali e conseguentemente dello sforzo normale nei conci.
L'analisi sismica nella direzione orizzontale consiste nell'applicazione di forze orizzontali nei conci crescenti secondo un moltiplicatore e nell'esecuzione, ad ogni passo, delle verifiche di sicurezza fino ad individuare il moltiplicatore di collasso, corrispondente al massimo valore del moltiplicatore applicabile alla struttura in esame. Durante il processo incrementale avviene infatti un degrado progressivo della capacità della struttura, consistente, dal punto di vista della stabilità, nella formazione consecutiva di cerniere fino ad un numero massimo che segna l'insorgere del meccanismo, il quale si manifesta in corrispondenza appunto del moltiplicatore di collasso.
A partire dal moltiplicatore di collasso, le relazioni che legano tra loro il moltiplicatore stesso, l'accelerazione strutturale e la massa partecipante consentono il calcolo della massima accelerazione orizzontale al suolo sostenibile, cioè della capacità in termini di PGA. Confrontando tale capacità con la domanda secondo Normativa (la PGA richiesta per SLV, dipendente dal sito di ubicazione dell'edificio e dalle ipotesi sulla probabilità di superamento dello stato limite) si ottiene l'indicatore di rischio sismico ζE. La capacità può anche essere espressa in termini di periodo di ritorno TR.
Il valore dell'accelerazione al suolo che investe l'edificio nella sua zona di ubicazione compare pertanto solo nell'elaborazione finale e nel confronto tra capacità e domanda, dopo l'analisi incrementale ed il calcolo del moltiplicatore di collasso. In altri termini, la domanda non entra nel processo di calcolo della capacità: questo invece non avviene quando si considera anche la componente sismica verticale, come illustrato nel seguito.
Per l'inclusione nell'analisi sismica della componente verticale è indispensabile definire la modalità con cui introdurre forze inerziali verticali all'interno della procedura incrementale con moltiplicatore orizzontale crescente.
A partire dal valore comune dell'accelerazione al suolo orizzontale e verticale, il moltiplicatore verticale αV è legato al moltiplicatore orizzontale a secondo lo stesso rapporto che lega tra loro accelerazione strutturale verticale e accelerazione strutturale orizzontale.
Con riferimento ad un concio di un arco sottoposto ad un carico P agente nel suo baricentro, considerando carichi statici e azioni sismiche orizzontali e verticali, le forze agenti durante un passo incrementale di analisi sismica caratterizzato dal moltiplicatore α in direzione orizzontale sono le seguenti: forza peso P, forza inerziale orizzontale αP (in figura: direzione e verso: +X) e forza inerziale verticale αVP.
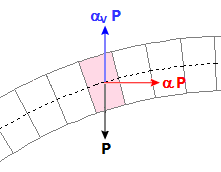
Mentre l'analisi incrementale viene considerata secondo un verso prefissato, +X o -X, l'incertezza sull'orientamento delle forze verticali rende necessario adottare diverse ipotesi di lavoro alla ricerca della situazione più sfavorevole. E' possibile proporre alcune analisi significative: un campo di forze equiverse verso l'alto, oppure equiverse verso il basso o dipendenti dal cinematismo.
L'ipotesi di verso delle forze verticali legato al cinematismo appare particolarmente significativa. Infatti, il meccanismo attivato dal moltiplicatore di collasso mostrerà un preciso campo di spostamento dei conci, con rotazioni cinematiche intorno alle cerniere formatesi nel corso dei degradi progressivi.
Alcuni gruppi di conci tenderanno a muoversi verso il basso, altri verso l'alto. Il campo di forze d'inerzia verticali a favore di sicurezza seguirà tale spostamento: gli effetti della componente sismica verticale saranno infatti massimi quando le corrispondenti forze tenderanno ad abbassare ancora più i conci che si abbassano (forze di aggravamento, verso il basso) e ad innalzare ancor più quelli che si innalzano (forze di alleggerimento, verso l'alto).
La forma esatta del meccanismo di collasso (cinematismo) è nota tuttavia solo ad analisi avvenuta, ma trattandosi di una struttura ad arco, con comportamento qualitativamente definibile a priori, è possibile evitare processi iterativi innescati sulla forma del cinematismo ipotizzando specifiche modalità secondo cui il cinematismo si manifesta nel verso di applicazione delle forze orizzontali.
Come risulta dall'immagine seguente, nel caso di sisma nel verso +X, ottenuto applicando solo azioni inerziali orizzontali, il meccanismo di collasso presenta un abbassamento nella parte sinistra e un innalzamento nella parte destra; nel caso -X avviene il viceversa.
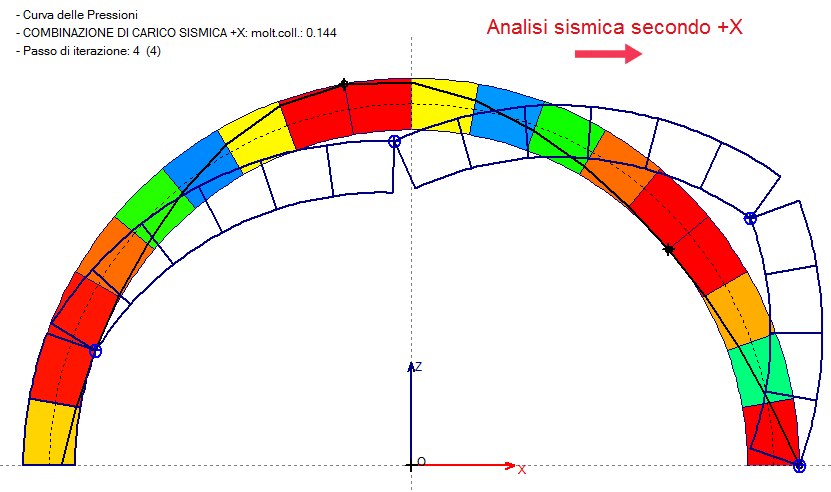
Tracciando quindi nella mezzeria della luce l'asse verticale dell'arco, si possono distinguere il gruppo di conci in abbassamento ulteriore sotto forze verticali verso il basso dall'altro gruppo con comportamento opposto. Questa modalità di applicazione delle forze sismiche verticali garantisce risultati a favore di sicurezza. Il campo di forze inerziali verticali che a favore di sicurezza può essere applicato sull'arco al fine di eseguire un'analisi sismica che tenga conto di entrambe le componenti orizzontale e verticale è rappresentato in figura seguente, ed è identificabile nelle ipotesi di SAV come campo di forze verticali dipendenti dal cinematismo.
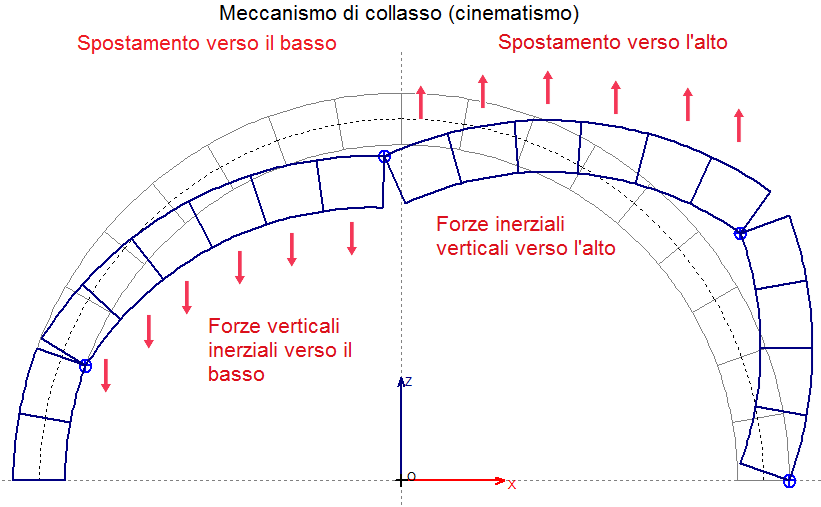
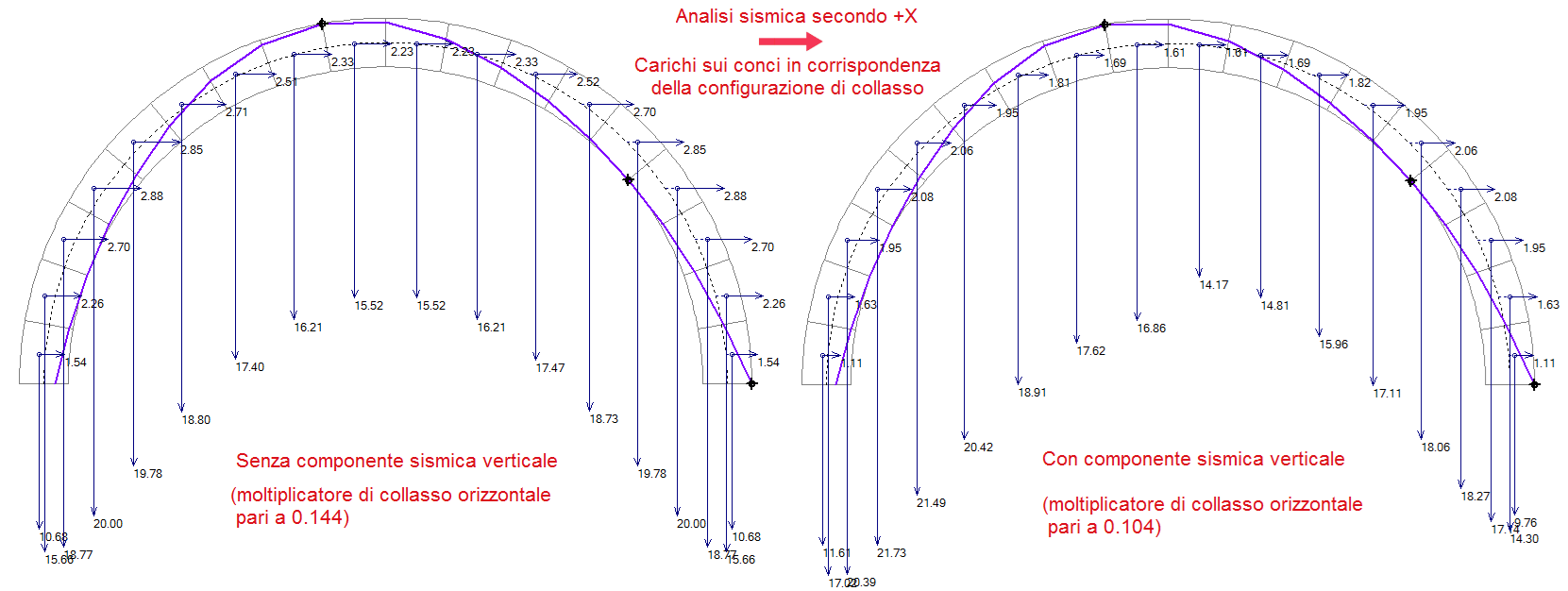
Nei casi applicativi si osserva che inserendo la componente sismica verticale l'indicatore di rischio sismico ζE si riduce per una percentuale simile alla riduzione del moltiplicatore di collasso, una riduzione che può essere significativa, come nell'esempio riportato nell'immagine soprastante.
In dipendenza dal tipo di volta, dai carichi e dalla zona di ubicazione della costruzione, nel campo del consolidamento strutturale si rende quindi opportuna l'inclusione della componente sismica verticale per valutare le implicazioni sui coefficienti di sicurezza e conseguentemente sulla definizione degli interventi di rinforzo.
